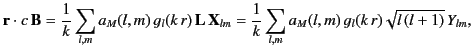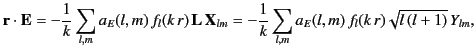Next: Properties of Multipole Fields
Up: Multipole Expansion
Previous: Angular Momentum Operators
Maxwell's equations in free space reduce to
assuming an
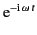 time dependence of all field
quantities. Here,
time dependence of all field
quantities. Here,
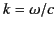 .
Eliminating
.
Eliminating  between Equations (1453) and (1454),
we obtain
between Equations (1453) and (1454),
we obtain
with  given by
given by
 |
(1455) |
Alternatively,  can be eliminated to give
can be eliminated to give
with  given by
given by
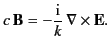 |
(1458) |
It is clear that each Cartesian component of  and
and  satisfies the homogeneous Helmholtz wave equation, (1413). Hence, according to the analysis of Section 11.2, these components
can be written as a general expansion of the form
satisfies the homogeneous Helmholtz wave equation, (1413). Hence, according to the analysis of Section 11.2, these components
can be written as a general expansion of the form
![$\displaystyle \psi({\bf r}) = \sum_{l,m}\left[A_{lm}^{(1)} \,h_l^{(1)}(k\,r) +A_{lm}^{(2)} \,h_l^{(2)}(k\,r)\right] Y_{lm}(\theta,\varphi),$](img3076.png) |
(1459) |
where 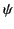 stands for any Cartesian component of
stands for any Cartesian component of  or
or  .
Note, however, that the three Cartesian components of
.
Note, however, that the three Cartesian components of  or
or
 are not entirely independent, because they must also satisfy
the constraints
are not entirely independent, because they must also satisfy
the constraints
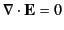 and
and
 . Let us examine how these constraints can be satisfied
with the minimum of effort.
. Let us examine how these constraints can be satisfied
with the minimum of effort.
Consider the scalar
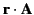 , where
, where 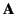 is a well-behaved vector field. It is easily verified that
is a well-behaved vector field. It is easily verified that
 |
(1460) |
It follows from Equations (1455)-(1456) and (1458)-(1459) that the scalars
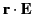 and
and
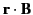 both satisfy the homogeneous Helmholtz wave equation: that is,
both satisfy the homogeneous Helmholtz wave equation: that is,
Thus, the general solutions for
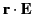 and
and
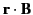 can be written in the form (1461).
can be written in the form (1461).
Let us define a magnetic multipole field of order 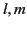 as the solution of
as the solution of
where
 |
(1465) |
The presence of the factor
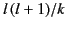 in Equation (1465) is for later convenience.
Equation (1460) yields
in Equation (1465) is for later convenience.
Equation (1460) yields
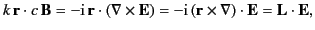 |
(1466) |
where 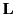 is given by Equation (1438). Thus, with
is given by Equation (1438). Thus, with
 taking the form (1465), the electric field associated with a magnetic
multipole must satisfy
taking the form (1465), the electric field associated with a magnetic
multipole must satisfy
 |
(1467) |
as well as
 . Recall that the operator
. Recall that the operator
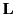 acts on the angular variables
acts on the angular variables
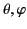 only.
This implies that the radial dependence of
only.
This implies that the radial dependence of
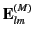 is given by
is given by 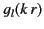 . It is easily seen from Equations (1436)
and (1442)
that the solution to Equations (1466) and (1469) can be written in the form
. It is easily seen from Equations (1436)
and (1442)
that the solution to Equations (1466) and (1469) can be written in the form
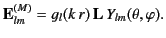 |
(1468) |
It follows from the analysis Section 11.3 that the angular dependence of
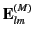 consists
of a linear combination of
consists
of a linear combination of
 ,
,
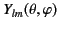 , and
, and
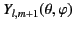 functions. Equation (1470),
together with
functions. Equation (1470),
together with
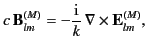 |
(1469) |
specifies the electromagnetic fields of a magnetic multipole of
order 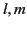 . According to Equation (1442), the electric field (1470) is transverse to the radius vector. Thus, magnetic multipole
fields are sometimes termed transverse electric (TE)
multipole fields.
. According to Equation (1442), the electric field (1470) is transverse to the radius vector. Thus, magnetic multipole
fields are sometimes termed transverse electric (TE)
multipole fields.
The fields of an electric, or transverse magnetic (TM),
multipole of order 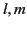 satisfy
satisfy
It follows that the fields of an electric multipole are
Here, the radial function 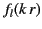 is an expression of the form
(1467).
is an expression of the form
(1467).
The two sets of multipole fields, (1470)-(1471), and (1474)-(1475), form a
complete set of vector solutions to Maxwell's equations in free space.
Because the vector spherical harmonic
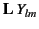 plays an important
role in the theory of multipole fields, it is convenient to introduce the normalized
form
plays an important
role in the theory of multipole fields, it is convenient to introduce the normalized
form
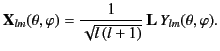 |
(1474) |
It can be demonstrated that these forms possess
the orthogonality properties
for all  ,
,  ,
,  , and
, and 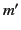 .
.
By combining the two types of multipole fields, we can write the general solution
to Maxwell's equations in free space as
where the coefficients 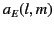 and
and 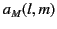 specify the
amounts of electric
specify the
amounts of electric 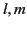 and magnetic
and magnetic 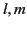 multipole fields.
The radial functions
multipole fields.
The radial functions 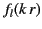 and
and 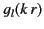 are both of the form (1467). The
coefficients
are both of the form (1467). The
coefficients 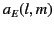 and
and 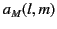 , as well as the relative
proportions of the two types of Hankel functions in the radial functions
, as well as the relative
proportions of the two types of Hankel functions in the radial functions 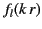 and
and 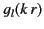 , are determined by the sources and
the boundary conditions.
, are determined by the sources and
the boundary conditions.
Equations (1479) and (1480) yield
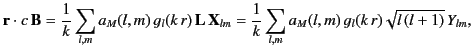 |
(1479) |
and
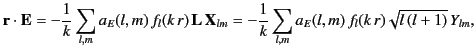 |
(1480) |
where use has been made of Equations (1436), (1438), (1442), and (1476).
It follows from the well-known orthogonality property of the spherical
harmonics that
Thus, knowledge of
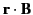 and
and
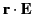 at two different radii in a source-free region permits
a complete specification of the fields, including the relative
proportions of the Hankel functions
at two different radii in a source-free region permits
a complete specification of the fields, including the relative
proportions of the Hankel functions
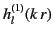 and
and
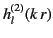 present in the
radial functions
present in the
radial functions 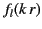 and
and
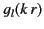 .
.



Next: Properties of Multipole Fields
Up: Multipole Expansion
Previous: Angular Momentum Operators
Richard Fitzpatrick
2014-06-27

![]() and
and ![]() satisfies the homogeneous Helmholtz wave equation, (1413). Hence, according to the analysis of Section 11.2, these components
can be written as a general expansion of the form
satisfies the homogeneous Helmholtz wave equation, (1413). Hence, according to the analysis of Section 11.2, these components
can be written as a general expansion of the form
![]() , where
, where ![]() is a well-behaved vector field. It is easily verified that
is a well-behaved vector field. It is easily verified that
![]() as the solution of
as the solution of
![]() satisfy
satisfy
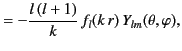
![]() plays an important
role in the theory of multipole fields, it is convenient to introduce the normalized
form
plays an important
role in the theory of multipole fields, it is convenient to introduce the normalized
form