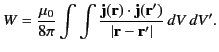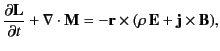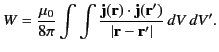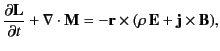Next: Electrostatic Fields
Up: Maxwell's Equations
Previous: Electromagnetic Momentum Conservation
- Demonstrate that the energy contained in the magnetic field generated by a stationary current distribution
 in vacuum
is given by
in vacuum
is given by
- A transverse plane wave is incident normally in vacuum on a perfectly absorbing flat screen. Show that the
pressure exerted on the screen is equal to the electromagnetic energy density of the wave.
- Consider an infinite parallel-plate capacitor. Let the lower plate lie at
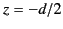 , and carry the charge density
, and carry the charge density 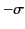 .
Likewise, let the upper plate lie at
.
Likewise, let the upper plate lie at 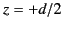 , and carry the charge density
, and carry the charge density 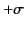 . Calculate the electromagnetic
momentum flux across the
. Calculate the electromagnetic
momentum flux across the 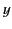 -
- plane. Hence, determine the direction and magnitude of the force per unit area
that the plates exert on one another.
plane. Hence, determine the direction and magnitude of the force per unit area
that the plates exert on one another.
- The equation of electromagnetic angular momentum conservation takes the general form
where 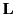 is the electromagnetic angular momentum density, and the tensor
is the electromagnetic angular momentum density, and the tensor 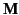 is the electromagnetic angular
momentum flux. Demonstrate
that
is the electromagnetic angular
momentum flux. Demonstrate
that
and
where  is the electromagnetic momentum density, and
is the electromagnetic momentum density, and 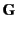 the electromagnetic momentum flux tensor.
the electromagnetic momentum flux tensor.
- A long solenoid of radius
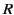 , with
, with 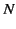 turn per unit length, carries a steady current
turn per unit length, carries a steady current 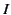 . Two hollow
cylinders of length
. Two hollow
cylinders of length  are fixed coaxially such that they are free to rotate. The first cylinder, whose radius is
are fixed coaxially such that they are free to rotate. The first cylinder, whose radius is 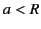 ,
carries the uniformly distributed electric charge
,
carries the uniformly distributed electric charge 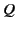 . The second cylinder, whose radius is
. The second cylinder, whose radius is  , carries the
uniformly distributed electric charge
, carries the
uniformly distributed electric charge 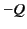 . Both cylinders are initially stationary. When the current is switched off the cylinders
start to rotate. Find the final angular momenta of the two cylinders, and demonstrate that the total angular momentum
of the system is the same before and after the current is switched off.
. Both cylinders are initially stationary. When the current is switched off the cylinders
start to rotate. Find the final angular momenta of the two cylinders, and demonstrate that the total angular momentum
of the system is the same before and after the current is switched off.
- Consider a system consisting of an electric charge
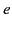 and a magnetic monopole
and a magnetic monopole 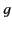 separated by a
distance
separated by a
distance 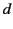 . Demonstrate that the total angular momentum stored in the resulting electromagnetic fields is
. Demonstrate that the total angular momentum stored in the resulting electromagnetic fields is
[Hint: The radial magnetic field generated a distance 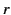 from a magnetic monopole of strength
from a magnetic monopole of strength 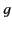 is of magnitude
is of magnitude
 .]
.]



Next: Electrostatic Fields
Up: Maxwell's Equations
Previous: Electromagnetic Momentum Conservation
Richard Fitzpatrick
2014-06-27