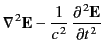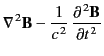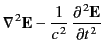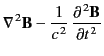Next: Resonant Cavities and Waveguides
Up: Radiation and Scattering
Previous: Rayleigh Scattering
- Consider an electromagnetic wave propagating through a
non-dielectric, non-magnetic medium containing free charge
density
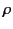 and free current density
and free current density  . Demonstrate
from Maxwell's equations that the associated wave equations
take the form
. Demonstrate
from Maxwell's equations that the associated wave equations
take the form
- A spherically symmetric charge distribution undergoes purely
radial oscillations. Show that no electromagnetic waves are emitted. [Hint: Show that there is no magnetic field.]
Richard Fitzpatrick
2014-06-27