


Next: Advanced potentials?
Up: Time-dependent Maxwell's equations
Previous: Green's functions
Retarded potentials
We are now in a position to solve Maxwell's equations. Recall that in
steady-state, Maxwell's
equations reduce to
The solutions to these equations are easily found using the Green's function for Poisson's
equation (480):
The time-dependent Maxwell equations reduce to
We can solve these equations using the time-dependent Green's function (499). From Eq. (486)
we find that
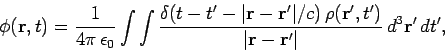 |
(508) |
with a similar equation for  . Using the well-known property of delta-functions,
these equations reduce to
. Using the well-known property of delta-functions,
these equations reduce to
These are the general solutions to Maxwell's equations. Note that the time-dependent solutions,
(509) and (510), are the same as the steady-state solutions,
(504) and (505), apart from the weird way in which
time appears in the former. According to
Eqs. (509) and (510), if we want to work out the potentials
at position 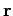 and time
and time 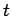 then we have to perform integrals of the charge density and current
density over all space (just like in the steady-state situation). However, when we calculate the
contribution of charges and currents at position
then we have to perform integrals of the charge density and current
density over all space (just like in the steady-state situation). However, when we calculate the
contribution of charges and currents at position 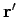 to these integrals we do not use
the values at time
to these integrals we do not use
the values at time 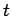 , instead we use the values at some earlier time
, instead we use the values at some earlier time
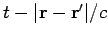 . What is this earlier time? It is simply the latest
time at which a light signal emitted from position
. What is this earlier time? It is simply the latest
time at which a light signal emitted from position 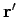 would be received at position
would be received at position
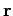 before time
before time 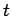 . This is called the retarded time. Likewise, the potentials
(509) and (510) are called retarded potentials. It is often useful to adopt the following notation
. This is called the retarded time. Likewise, the potentials
(509) and (510) are called retarded potentials. It is often useful to adopt the following notation
![\begin{displaymath}
A({\bf r}', t- \vert{\bf r} - {\bf r}'\vert/c) \equiv \left[ A({\bf r}', t)\right].
\end{displaymath}](img1134.png) |
(511) |
The square brackets denote retardation (i.e., using the retarded time instead of the real time).
Using this notation Eqs. (509) and (510), become
The time dependence in the above equations is taken as read.
We are now in a position to understand electromagnetism at its most fundamental level.
A charge distribution
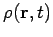 can thought of as built up
out of a collection, or series, of charges which
instantaneously come into existence, at some point
can thought of as built up
out of a collection, or series, of charges which
instantaneously come into existence, at some point 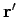 and some time
and some time 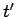 , and
then disappear again. Mathematically, this is written
, and
then disappear again. Mathematically, this is written
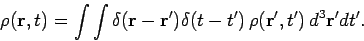 |
(514) |
Likewise, we can think of a current distribution
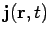 as built up
out of a collection or series of currents which instantaneously appear and then disappear:
as built up
out of a collection or series of currents which instantaneously appear and then disappear:
 |
(515) |
Each of these ephemeral charges and currents excites a spherical wave in the appropriate
potential. Thus, the charge density at 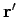 and
and 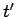 sends out a wave in the
scalar potential:
sends out a wave in the
scalar potential:
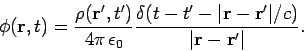 |
(516) |
Likewise, the current density at 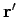 and
and 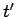 sends out a wave in the vector potential:
sends out a wave in the vector potential:
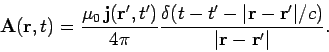 |
(517) |
These waves can be thought of as messengers which inform other charges and currents about
the charges and currents present at position 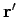 and time
and time 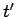 . However, these
messengers travel at a finite speed: i.e.,
the speed of light. So, by the time they reach other charges
and currents their message is a little out of date. Every charge and every current in the Universe
emits these spherical waves. The resultant scalar and vector
potential fields are given by Eqs. (512) and (513). Of course, we can turn these fields into
electric and magnetic fields using Eqs. (421) and
(422). We can then evaluate the force exerted on charges
using the Lorentz formula. We can see that we have now escaped from the apparent action at a distance
nature of Coulomb's law and the Biot-Savart law. Electromagnetic information
is carried by spherical waves in the vector and scalar potentials, and, therefore, travels at the
velocity of light. Thus, if we change the position of a charge then a distant charge can only
respond after a time delay sufficient for a spherical wave to propagate from the former to
the latter charge.
. However, these
messengers travel at a finite speed: i.e.,
the speed of light. So, by the time they reach other charges
and currents their message is a little out of date. Every charge and every current in the Universe
emits these spherical waves. The resultant scalar and vector
potential fields are given by Eqs. (512) and (513). Of course, we can turn these fields into
electric and magnetic fields using Eqs. (421) and
(422). We can then evaluate the force exerted on charges
using the Lorentz formula. We can see that we have now escaped from the apparent action at a distance
nature of Coulomb's law and the Biot-Savart law. Electromagnetic information
is carried by spherical waves in the vector and scalar potentials, and, therefore, travels at the
velocity of light. Thus, if we change the position of a charge then a distant charge can only
respond after a time delay sufficient for a spherical wave to propagate from the former to
the latter charge.
Let us compare the steady-state law
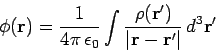 |
(518) |
with the corresponding time-dependent law
![\begin{displaymath}
\phi({\bf r}) = \frac{1}{4\pi \epsilon_0} \int\frac{\left[\...
...{\bf r'})\right]}
{\vert{\bf r} - {\bf r'}\vert}
d^3{\bf r'}
\end{displaymath}](img1144.png) |
(519) |
These two formulae look very similar indeed, but there is an important difference. We can imagine
(rather pictorially) that every
charge in the Universe is continuously performing the integral (519), and is
also performing a similar integral
to find the vector potential. After evaluating both potentials, the charge can calculate the
fields, and, using the Lorentz force law, it can then work out its equation of motion.
The problem is that
the information the charge receives from the rest of the Universe is carried by our spherical
waves, and is always slightly out of date (because the waves travel at a finite speed).
As the charge considers more and more distant charges or currents, its information
gets more and more out of date. (Similarly, when astronomers look out to more and more
distant galaxies in the Universe,
they are also looking backwards in time. In fact, the light we receive from the
most distant observable galaxies was emitted when the Universe was only about one third
of its present age.) So, what does our electron do? It simply uses the most up to date information
about distant charges and currents which it possesses.
So, instead of incorporating the charge density
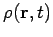 in its integral, the electron uses the retarded
charge density
in its integral, the electron uses the retarded
charge density
![$[\rho({\bf r}, t)]$](img1145.png) (i.e., the density
evaluated at the retarded time). This is effectively what Eq. (519) says.
(i.e., the density
evaluated at the retarded time). This is effectively what Eq. (519) says.
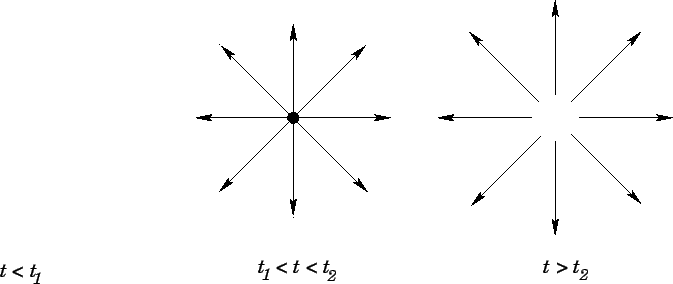
Consider a thought experiment in which a charge 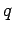 appears at position
appears at position 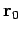 at time
at time
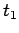 , persists for a while, and then disappears at time
, persists for a while, and then disappears at time 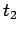 . What is the electric field
generated by such a charge? Using Eq. (519), we find that
. What is the electric field
generated by such a charge? Using Eq. (519), we find that
Now,
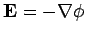 (since there are no currents, and therefore no vector potential
is generated), so
(since there are no currents, and therefore no vector potential
is generated), so
This solution is shown pictorially in Fig. 37. We can see that the charge effectively emits
a Coulomb electric field which propagates radially away from the charge at the speed of
light. Likewise, it is easy to show that a current carrying wire effectively emits an Ampèrian
magnetic field at the speed of light.
Figure 37:
 |
We can now appreciate the essential difference between time-dependent electromagnetism and
the action at a distance laws of Coulomb and Biot & Savart. In the latter
theories, the field-lines act
rather like rigid
wires attached to charges (or circulating around currents). If the charges (or currents) move then
so do the field-lines, leading inevitably to unphysical action at a distance type behaviour.
In the time-dependent theory, charges act rather like water sprinklers: i.e., they spray out the
Coulomb field in all directions at the speed of light. Similarly,
current carrying wires throw out magnetic field
loops at the speed of light. If we move a charge (or current) then field-lines emitted beforehand
are not affected, so the field at a distant charge (or current) only responds to the change
in position
after a time delay sufficient for the field to propagate between the two charges (or currents) at
the speed of light.
In Coulomb's law and the Biot-Savart law, it is not entirely obvious that the electric and magnetic fields
have a real existence. After all, the only measurable quantities are the forces acting between charges and
currents. We can describe the force acting on a given charge or current, due to the other charges
and currents in the Universe,
in terms of the local electric and magnetic fields, but we have no way of knowing whether these
fields persist when the charge or current is not present (i.e., we could argue that electric and
magnetic fields are just a convenient way of calculating forces, but, in reality, the forces
are transmitted directly between charges and currents by some form of magic).
However, it is patently obvious that electric and magnetic fields have a real existence
in the time-dependent theory. Consider the following thought experiment.
Suppose that a charge  comes into existence for a period of time, emits a Coulomb
field, and then disappears. Suppose that a distant charge
comes into existence for a period of time, emits a Coulomb
field, and then disappears. Suppose that a distant charge 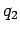 interacts with this field,
but is sufficiently far from the first charge that by the time the field arrives the
first charge has already disappeared. The force exerted on the second charge is only ascribable
to the electric field: it cannot be ascribed to the first charge, because this charge no longer exists
by the time the force is exerted. The electric field clearly transmits energy and momentum
between the two charges. Anything which possesses energy and momentum is ``real'' in a physical
sense. Later on in this course, we shall demonstrate that electric and magnetic fields conserve
energy and momentum.
interacts with this field,
but is sufficiently far from the first charge that by the time the field arrives the
first charge has already disappeared. The force exerted on the second charge is only ascribable
to the electric field: it cannot be ascribed to the first charge, because this charge no longer exists
by the time the force is exerted. The electric field clearly transmits energy and momentum
between the two charges. Anything which possesses energy and momentum is ``real'' in a physical
sense. Later on in this course, we shall demonstrate that electric and magnetic fields conserve
energy and momentum.
Figure 38:
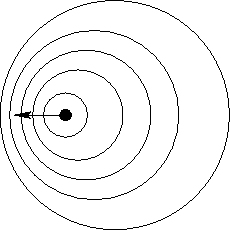 |
Let us now consider a moving charge. Such a charge is continually emitting spherical waves in the
scalar potential, and the resulting wavefront pattern is sketched in Fig. 38.
Clearly, the wavefronts are more closely spaced in front of the charge than they are
behind it, suggesting
that the electric field in front is larger than the field behind.
In a medium, such as water or air, where
waves travel at a finite speed, 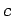 (say), it is possible to get a very interesting effect
if the wave source travels at some velocity
(say), it is possible to get a very interesting effect
if the wave source travels at some velocity 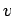 which exceeds the wave speed. This
is illustrated in Fig. 39.
which exceeds the wave speed. This
is illustrated in Fig. 39.
Figure 39:
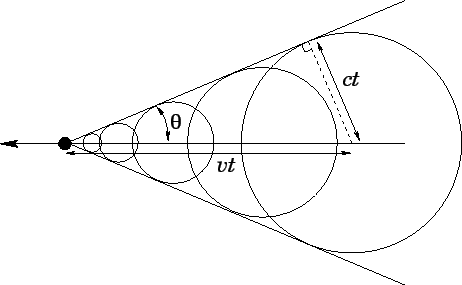 |
The locus of the outermost wave front is now a cone instead of a sphere.
The wave intensity on the cone is extremely large: this is a shock wave! The half-angle 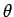 of the shock wave cone is simply
of the shock wave cone is simply
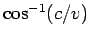 . In water, shock waves are produced by fast moving
boats. We call these bow waves. In air, shock waves are produced by speeding bullets
and supersonic jets. In the latter case, we call these sonic booms. Is there any such thing
as an electromagnetic shock wave? At first sight, the answer to this question would appear to
be, no. After all, electromagnetic waves travel at the speed of light, and no wave source
(i.e., an electrically charged particle) can travel faster than this velocity. This is
a rather disappointing conclusion. However, when an electromagnetic wave travels through matter
a remarkable thing happens. The oscillating electric field of the wave induces a slight
separation of the positive and negative charges in the atoms which
make up the material. We call separated positive and negative charges an electric
dipole. Of course, the atomic dipoles oscillate in sympathy
with the field which induces them. However, an oscillating electric dipole radiates electromagnetic
waves. Amazingly, when we add the original wave to these induced waves, it is exactly as if
the original wave propagates through the material in question at a velocity which is
slower than the velocity of light in vacuum.
Suppose, now, that we shoot a charged particle through the material faster than the slowed down
velocity of electromagnetic waves. This is possible since the waves are traveling slower
than the velocity of light in vacuum. In practice, the particle has to be traveling pretty
close to the velocity of
light in vacuum (i.e., it has to be relativistic), but modern particle accelerators produce
copious amounts of such particles. Now, we can get an electromagnetic shock wave. We expect
an intense cone of emission, just like the bow wave produced by a fast ship. In fact, this
type of
radiation has been observed. It is called Cherenkov radiation, and it is very useful in
high energy physics. Cherenkov radiation is typically produced by surrounding a particle accelerator
with perspex blocks. Relativistic charged particles emanating from the accelerator pass through the perspex
traveling faster than the local velocity of light, and therefore emit
Cherenkov radiation. We know the velocity of light (
. In water, shock waves are produced by fast moving
boats. We call these bow waves. In air, shock waves are produced by speeding bullets
and supersonic jets. In the latter case, we call these sonic booms. Is there any such thing
as an electromagnetic shock wave? At first sight, the answer to this question would appear to
be, no. After all, electromagnetic waves travel at the speed of light, and no wave source
(i.e., an electrically charged particle) can travel faster than this velocity. This is
a rather disappointing conclusion. However, when an electromagnetic wave travels through matter
a remarkable thing happens. The oscillating electric field of the wave induces a slight
separation of the positive and negative charges in the atoms which
make up the material. We call separated positive and negative charges an electric
dipole. Of course, the atomic dipoles oscillate in sympathy
with the field which induces them. However, an oscillating electric dipole radiates electromagnetic
waves. Amazingly, when we add the original wave to these induced waves, it is exactly as if
the original wave propagates through the material in question at a velocity which is
slower than the velocity of light in vacuum.
Suppose, now, that we shoot a charged particle through the material faster than the slowed down
velocity of electromagnetic waves. This is possible since the waves are traveling slower
than the velocity of light in vacuum. In practice, the particle has to be traveling pretty
close to the velocity of
light in vacuum (i.e., it has to be relativistic), but modern particle accelerators produce
copious amounts of such particles. Now, we can get an electromagnetic shock wave. We expect
an intense cone of emission, just like the bow wave produced by a fast ship. In fact, this
type of
radiation has been observed. It is called Cherenkov radiation, and it is very useful in
high energy physics. Cherenkov radiation is typically produced by surrounding a particle accelerator
with perspex blocks. Relativistic charged particles emanating from the accelerator pass through the perspex
traveling faster than the local velocity of light, and therefore emit
Cherenkov radiation. We know the velocity of light (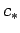 , say)
in perspex (this can be worked out from the
refractive index), so if we can measure the half angle
, say)
in perspex (this can be worked out from the
refractive index), so if we can measure the half angle 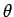 of the radiation cone
emitted by each particle
then we can evaluate the speed of the particle
of the radiation cone
emitted by each particle
then we can evaluate the speed of the particle 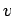 via the geometric relation
via the geometric relation
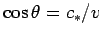 .
.



Next: Advanced potentials?
Up: Time-dependent Maxwell's equations
Previous: Green's functions
Richard Fitzpatrick
2006-02-02
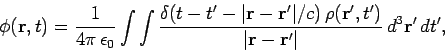
![]() can thought of as built up
out of a collection, or series, of charges which
instantaneously come into existence, at some point
can thought of as built up
out of a collection, or series, of charges which
instantaneously come into existence, at some point ![]() and some time
and some time ![]() , and
then disappear again. Mathematically, this is written
, and
then disappear again. Mathematically, this is written
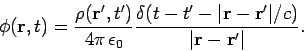
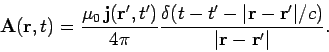
![]() appears at position
appears at position ![]() at time
at time
![]() , persists for a while, and then disappears at time
, persists for a while, and then disappears at time ![]() . What is the electric field
generated by such a charge? Using Eq. (519), we find that
. What is the electric field
generated by such a charge? Using Eq. (519), we find that
![]() comes into existence for a period of time, emits a Coulomb
field, and then disappears. Suppose that a distant charge
comes into existence for a period of time, emits a Coulomb
field, and then disappears. Suppose that a distant charge ![]() interacts with this field,
but is sufficiently far from the first charge that by the time the field arrives the
first charge has already disappeared. The force exerted on the second charge is only ascribable
to the electric field: it cannot be ascribed to the first charge, because this charge no longer exists
by the time the force is exerted. The electric field clearly transmits energy and momentum
between the two charges. Anything which possesses energy and momentum is ``real'' in a physical
sense. Later on in this course, we shall demonstrate that electric and magnetic fields conserve
energy and momentum.
interacts with this field,
but is sufficiently far from the first charge that by the time the field arrives the
first charge has already disappeared. The force exerted on the second charge is only ascribable
to the electric field: it cannot be ascribed to the first charge, because this charge no longer exists
by the time the force is exerted. The electric field clearly transmits energy and momentum
between the two charges. Anything which possesses energy and momentum is ``real'' in a physical
sense. Later on in this course, we shall demonstrate that electric and magnetic fields conserve
energy and momentum.