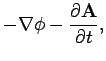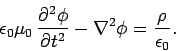Next: The displacement current
Up: Time-dependent Maxwell's equations
Previous: Electric scalar potential?
Gauge transformations
Electric and magnetic fields can be written in terms of scalar and
vector potentials, as follows:
However, this prescription is not unique. There are many different
potentials which can generate the same fields. We have come
across this problem before. It is called gauge invariance. The most general
transformation which leaves the 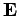 and
and 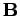 fields unchanged in
Eqs. (385) and (386) is
fields unchanged in
Eqs. (385) and (386) is
This is clearly a generalization of the gauge transformation
which we found earlier for static fields:
where 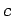 is a constant.
In fact, if
is a constant.
In fact, if
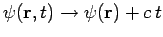 then Eqs. (387) and (388) reduce
to Eqs. (389) and (390).
then Eqs. (387) and (388) reduce
to Eqs. (389) and (390).
We are free to choose the gauge so as to make our equations as simple
as possible. As before, the most sensible gauge for the scalar potential is
to make it go to zero at infinity:
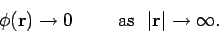 |
(391) |
For steady fields, we found that
the optimum gauge for the vector potential
was the so-called Coulomb gauge:
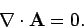 |
(392) |
We can still use this gauge for non-steady fields. The argument which we gave
earlier (see Sect. 3.12), that it is always possible to transform away the
divergence of a vector potential, remains valid. One of the nice features of
the Coulomb gauge is that when we write the electric field,
 |
(393) |
we find that the part which is generated by charges (i.e., the first term on the
right-hand side) is conservative, and the part induced by magnetic fields
(i.e., the second term on the right-hand side) is purely solenoidal. Earlier on, we
proved mathematically that a general vector field can be written as the sum
of a conservative field and a solenoidal field (see Sect. 3.11). Now we
are finding that when we split up the electric field in this manner the
two fields have different physical origins: the conservative part of
the field emanates from
electric charges, whereas the solenoidal part is induced by magnetic fields.
Equation (393) can be combined with the field equation
 |
(394) |
(which remains valid for non-steady fields) to give
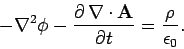 |
(395) |
With the Coulomb gauge condition,
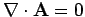 , the above expression
reduces to
, the above expression
reduces to
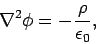 |
(396) |
which is just Poisson's equation. Thus, we can immediately write down an expression
for the scalar potential generated by non-steady fields. It is exactly the same
as our previous expression for the scalar potential generated by steady fields,
namely
 |
(397) |
However, this apparently simple result is extremely deceptive.
Equation (397) is a typical action at a distance law. If the charge density changes
suddenly at 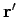 then the potential at
then the potential at 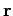 responds immediately.
However, we shall see later that the full time-dependent Maxwell's equations only
allow information to propagate at the speed of light (i.e., they do not violate
relativity). How can these two statements be reconciled? The crucial point is
that the scalar potential cannot be measured directly, it can only be inferred
from the electric field. In the time-dependent case, there are two parts to the
electric field: that part which comes from the scalar potential, and that part
which comes from the vector potential [see Eq. (393)]. So, if the scalar
potential responds immediately to some distance rearrangement of charge density
it does not necessarily follow that the electric field also has an immediate response.
What actually happens is that the change in the part of the
electric field which comes from
the scalar
potential is balanced by an equal and opposite change in the part which comes from the
vector potential, so that the overall electric field remains unchanged. This state
of affairs persists at least until sufficient time has elapsed for a light
signal to travel from the distant charges to the region in question.
Thus, relativity is not violated, since it is the
electric field, and not the scalar potential, which carries physically accessible
information.
responds immediately.
However, we shall see later that the full time-dependent Maxwell's equations only
allow information to propagate at the speed of light (i.e., they do not violate
relativity). How can these two statements be reconciled? The crucial point is
that the scalar potential cannot be measured directly, it can only be inferred
from the electric field. In the time-dependent case, there are two parts to the
electric field: that part which comes from the scalar potential, and that part
which comes from the vector potential [see Eq. (393)]. So, if the scalar
potential responds immediately to some distance rearrangement of charge density
it does not necessarily follow that the electric field also has an immediate response.
What actually happens is that the change in the part of the
electric field which comes from
the scalar
potential is balanced by an equal and opposite change in the part which comes from the
vector potential, so that the overall electric field remains unchanged. This state
of affairs persists at least until sufficient time has elapsed for a light
signal to travel from the distant charges to the region in question.
Thus, relativity is not violated, since it is the
electric field, and not the scalar potential, which carries physically accessible
information.
It is clear that the apparent action at a distance
nature of Eq. (397) is highly misleading. This suggests, very strongly, that the
Coulomb gauge is not the optimum gauge in the time-dependent case. A more
sensible choice is the so called Lorentz gauge:
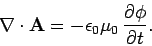 |
(398) |
It can be shown, by analogy with earlier arguments (see Sect. 3.12), that
it
is always possible to make a gauge transformation, at a given instance in time,
such that the above equation is satisfied. Substituting the Lorentz gauge condition
into Eq. (395), we obtain
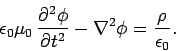 |
(399) |
It turns out that this is a three-dimensional wave equation in which information
propagates at the speed of light. But, more of this later.
Note that the magnetically induced part of
the electric field (i.e.,
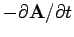 )
is not purely solenoidal in the Lorentz
gauge. This is a slight disadvantage of the Lorentz gauge with respect to the
Coulomb gauge. However, this disadvantage
is more than offset by other advantages which will
become apparent presently. Incidentally, the fact that the part of the electric
field which we
ascribe to magnetic induction changes when we change the gauge suggests
that the separation
of the field into magnetically induced and charge induced components is not
unique in the general time-varying case (i.e., it is a convention).
)
is not purely solenoidal in the Lorentz
gauge. This is a slight disadvantage of the Lorentz gauge with respect to the
Coulomb gauge. However, this disadvantage
is more than offset by other advantages which will
become apparent presently. Incidentally, the fact that the part of the electric
field which we
ascribe to magnetic induction changes when we change the gauge suggests
that the separation
of the field into magnetically induced and charge induced components is not
unique in the general time-varying case (i.e., it is a convention).



Next: The displacement current
Up: Time-dependent Maxwell's equations
Previous: Electric scalar potential?
Richard Fitzpatrick
2006-02-02