


Next: Magnetic monopoles?
Up: Time-independent Maxwell equations
Previous: The Lorentz force
Magnetic fields, like electric fields, are completely superposable. So, if
a field 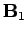 is generated by a current
is generated by a current 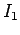 flowing through some circuit,
and a field
flowing through some circuit,
and a field 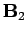 is generated by a current
is generated by a current 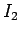 flowing through another
circuit, then when the currents
flowing through another
circuit, then when the currents 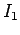 and
and 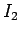 flow through both circuits
simultaneously the generated magnetic field is
flow through both circuits
simultaneously the generated magnetic field is
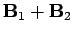 .
.
Figure 30:
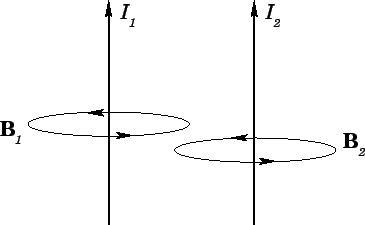 |
Consider two parallel wires separated by a perpendicular distance 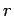 and carrying electric currents
and carrying electric currents 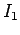 and
and 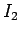 , respectively (see Fig. 30). The magnetic field
strength at the second wire due to the current flowing in the first wire
is
, respectively (see Fig. 30). The magnetic field
strength at the second wire due to the current flowing in the first wire
is
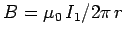 . This field is orientated at right-angles to the second
wire, so the force per unit length exerted on the second wire is
. This field is orientated at right-angles to the second
wire, so the force per unit length exerted on the second wire is
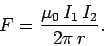 |
(253) |
This follows from Eq. (229), which is valid for continuous wires as well as short
test wires. The force acting on the second wire is directed radially inwards towards
the first wire. The magnetic field strength at the first wire due to the
current flowing in the second wire is
 . This field
is orientated at right-angles to the first wire, so the force per unit length acting
on the first wire is equal and opposite to that acting on the second wire,
according to Eq. (229). Equation (253) is sometimes called Ampère's law,
and is clearly another example of an action at a distance law: i.e., if the
current in the first wire is suddenly changed then the force on the second wire
immediately adjusts. In reality, there should be a short time delay, at
least as long as the propagation time for a light signal between the two wires.
Clearly, Ampère's law is not strictly correct. However, as long as we restrict
our investigations to steady currents it is perfectly adequate.
. This field
is orientated at right-angles to the first wire, so the force per unit length acting
on the first wire is equal and opposite to that acting on the second wire,
according to Eq. (229). Equation (253) is sometimes called Ampère's law,
and is clearly another example of an action at a distance law: i.e., if the
current in the first wire is suddenly changed then the force on the second wire
immediately adjusts. In reality, there should be a short time delay, at
least as long as the propagation time for a light signal between the two wires.
Clearly, Ampère's law is not strictly correct. However, as long as we restrict
our investigations to steady currents it is perfectly adequate.



Next: Magnetic monopoles?
Up: Time-independent Maxwell equations
Previous: The Lorentz force
Richard Fitzpatrick
2006-02-02
