| (161) |
| (162) |
Coulomb's law has the same mathematical form as Newton's law of gravity.
Suppose that two masses, ![]() and
and ![]() , are located at position vectors
, are located at position vectors
![]() and
and ![]() . The gravitational force acting on the second mass
is written
. The gravitational force acting on the second mass
is written
| (164) |
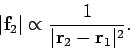 |
(165) |
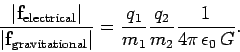 |
(166) |
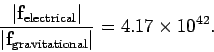 |
(167) |
In summary, there are two long-range forces in the Universe, electromagnetism and gravity. The former is enormously stronger than the latter, but is usually ``hidden'' away inside neutral atoms. The fine balance of forces due to negative and positive electric charges starts to break down on atomic scales. In fact, interatomic and intermolecular forces are all electrical in nature. So, electrical forces are basically what prevent us from falling though the floor. But, this is electromagnetism on the microscopic or atomic scale--what is usually termed quantum electromagnetism. This course is about classical electromagnetism. That is, electromagnetism on length-scales much larger than the atomic scale. Classical electromagnetism generally describes phenomena in which some sort of ``violence'' is done to matter, so that the close pairing of negative and positive charges is disrupted. This allows electrical forces to manifest themselves on macroscopic length-scales. Of course, very little disruption is necessary before gigantic forces are generated. It is no coincidence that the vast majority of useful machines which humankind has devised during the last century or so are electrical in nature.
Coulomb's law and Newton's law are both examples of what are usually referred to as action at a distance theories. According to Eqs. (161) and (163), if the first charge or mass is moved then the force acting on the second charge or mass immediately responds. In particular, equal and opposite forces act on the two charges or masses at all times. However, this cannot be correct according to Einstein's theory of relativity, which implies that the maximum speed with which information can propagate through the Universe is the speed of light in vacuum. So, if the first charge or mass is moved then there must always be time delay (i.e., at least the time needed for a light signal to propagate between the two charges or masses) before the second charge or mass responds. Consider a rather extreme example. Suppose the first charge or mass is suddenly annihilated. The second charge or mass only finds out about this some time later. During this time interval, the second charge or mass experiences an electrical or gravitational force which is as if the first charge or mass were still there. So, during this period, there is an action but no reaction, which violates Newton's third law of motion. It is clear that action at a distance is not compatible with relativity, and, consequently, that Newton's third law of motion is not strictly true. Of course, Newton's third law is intimately tied up with the conservation of linear momentum in the Universe. This is a concept which most physicists are loath to abandon. It turns out that we can ``rescue'' momentum conservation by abandoning action at a distance theories, and instead adopting so-called field theories in which there is a medium, called a field, which transmits the force from one particle to another. In electromagnetism there are, in fact, two fields--the electric field, and the magnetic field. Electromagnetic forces are transmitted via these fields at the speed of light, which implies that the laws of relativity are never violated. Moreover, the fields can soak up energy and momentum. This means that even when the actions and reactions acting on particles are not quite equal and opposite, momentum is still conserved. We can bypass some of the problematic aspects of action at a distance by only considering steady-state situations. For the moment, this is how we shall proceed.
Consider ![]() charges,
charges, ![]() though
though ![]() , which are located at position vectors
, which are located at position vectors
![]() through
through ![]() . Electrical forces obey what is known as
the principle of superposition. The electrical force acting on a test charge
. Electrical forces obey what is known as
the principle of superposition. The electrical force acting on a test charge
![]() at position vector
at position vector ![]() is simply the vector sum of all of the
Coulomb law forces from each of the
is simply the vector sum of all of the
Coulomb law forces from each of the ![]() charges taken in isolation. In other
words, the electrical force exerted by the
charges taken in isolation. In other
words, the electrical force exerted by the ![]() th charge (say) on the test charge is
the same as if all the other charges were not there. Thus, the force acting
on the test charge is given by
th charge (say) on the test charge is
the same as if all the other charges were not there. Thus, the force acting
on the test charge is given by
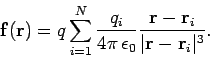 |
(168) |
The electric field from a single charge ![]() located at the origin is purely radial,
points outwards if the charge is positive, inwards if it is negative, and has
magnitude
located at the origin is purely radial,
points outwards if the charge is positive, inwards if it is negative, and has
magnitude
We can represent an electric field by field-lines. The direction of the lines indicates the direction of the local electric field, and the density of the lines perpendicular to this direction is proportional to the magnitude of the local electric field. Thus, the field of a point positive charge is represented by a group of equally spaced straight lines radiating from the charge (see Fig. 25).
The electric field from a collection of charges is
simply the vector sum of the fields
from each of the charges taken in isolation. In other words, electric fields are
completely superposable. Suppose that, instead of having discrete charges, we
have a continuous distribution of charge represented by a charge density
![]() . Thus, the charge at position vector
. Thus, the charge at position vector ![]() is
is
![]() , where
, where ![]() is the volume element
at
is the volume element
at ![]() . It follows from a simple extension of Eq. (170) that the electric
field generated by this charge distribution is
. It follows from a simple extension of Eq. (170) that the electric
field generated by this charge distribution is