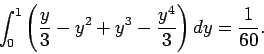Next: Vector surface integrals
Up: Vectors
Previous: Vector line integrals
Let us take a surface  , which is not necessarily co-planar, and divide in up
into (scalar) elements
, which is not necessarily co-planar, and divide in up
into (scalar) elements  . Then
. Then
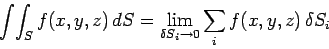 |
(75) |
is a surface integral. For instance, the volume of water in a lake of depth
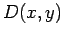 is
is
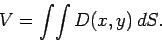 |
(76) |
To evaluate this integral we must split the calculation into two ordinary integrals.
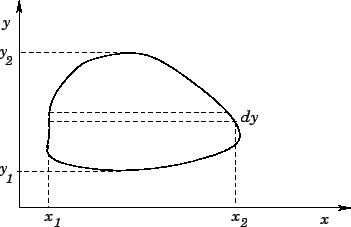
The volume in the strip shown in Fig. 14 is
![\begin{displaymath}
\left[\int_{x_1}^{x_2} D(x,y) dx\right] dy.
\end{displaymath}](img264.png) |
(77) |
Note that the limits 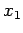 and
and 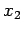 depend on
depend on  . The total volume is the sum
over all strips:
. The total volume is the sum
over all strips:
![\begin{displaymath}
V = \int_{y_1}^{y_2} dy\left[\int_{x_1(y)}^{x_2(y)} D(x,y) dx\right]
\equiv \int\!\int_S D(x,y) dx dy.
\end{displaymath}](img267.png) |
(78) |
Of course, the integral can be evaluated by taking the strips the other way around:
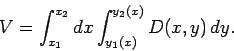 |
(79) |
Interchanging the order of integration is a very powerful and useful trick. But
great care must be taken when evaluating the limits.
Figure 14:
 |
As an example, consider
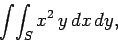 |
(80) |
where  is shown in Fig. 15.
Suppose that we evaluate the
is shown in Fig. 15.
Suppose that we evaluate the  integral first:
integral first:
![\begin{displaymath}
dy\left(\int_0^{1-y} x^2 y dx\right) = y dy\left[ \frac{x^3}{3}\right]^{1-y}_0
= \frac{y}{3} (1-y)^3 dy.
\end{displaymath}](img271.png) |
(81) |
Let us now evaluate the  integral:
integral:
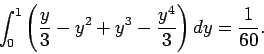 |
(82) |
We can also evaluate the integral by interchanging the order of integration:
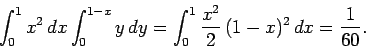 |
(83) |
Figure 15:
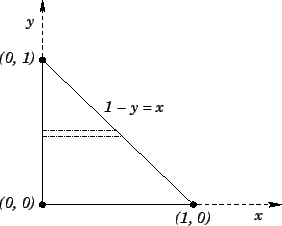 |
In some cases, a surface integral is just the product of two separate integrals.
For instance,
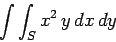 |
(84) |
where  is a unit square. This integral can be written
is a unit square. This integral can be written
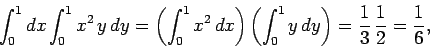 |
(85) |
since the limits are both independent of the other variable.
In general, when interchanging the order of integration, the most important part of
the whole problem is getting the limits of integration right. The only foolproof
way of doing this is to draw a diagram.



Next: Vector surface integrals
Up: Vectors
Previous: Vector line integrals
Richard Fitzpatrick
2006-02-02
![\begin{displaymath}
V = \int_{y_1}^{y_2} dy\left[\int_{x_1(y)}^{x_2(y)} D(x,y) dx\right]
\equiv \int\!\int_S D(x,y) dx dy.
\end{displaymath}](img267.png)
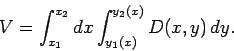
![\begin{displaymath}
dy\left(\int_0^{1-y} x^2 y dx\right) = y dy\left[ \frac{x^3}{3}\right]^{1-y}_0
= \frac{y}{3} (1-y)^3 dy.
\end{displaymath}](img271.png)