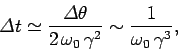Next: About this document ...
Up: Relativity and electromagnetism
Previous: Angular distribution of radiation
Synchrotron radiation (i.e., radiation emitted by a charged particle
constrained to follow a circular orbit by a magnetic field) is of
particular importance in astrophysics, since much of the
observed radio frequency
emission from supernova remnants and active galactic nuclei is thought to
be of this type.
Consider a charged particle moving in a circle of radius  with constant
angular velocity
with constant
angular velocity 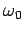 . Suppose that the orbit lies in the
. Suppose that the orbit lies in the  -
- plane. The radius vector pointing from the centre of the orbit
to the retarded position of the charge is defined
plane. The radius vector pointing from the centre of the orbit
to the retarded position of the charge is defined
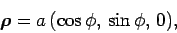 |
(1667) |
where
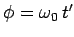 is the angle subtended between this vector
and the
is the angle subtended between this vector
and the  -axis. The retarded velocity and acceleration of the
charge take the form
-axis. The retarded velocity and acceleration of the
charge take the form
where 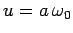 and
and
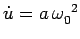 .
The observation point is chosen such that the radius vector
.
The observation point is chosen such that the radius vector 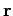 ,
pointing from the retarded position of the charge to the observation point,
is
parallel to the
,
pointing from the retarded position of the charge to the observation point,
is
parallel to the  -
- plane. Thus, we can write
plane. Thus, we can write
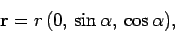 |
(1670) |
where 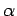 is the angle subtended between this vector
and the
is the angle subtended between this vector
and the  -axis.
As usual, we define
-axis.
As usual, we define 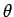 as the angle subtended between the retarded
radius vector
as the angle subtended between the retarded
radius vector 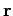 and the retarded direction of motion of
the charge
and the retarded direction of motion of
the charge 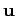 . It follows that
. It follows that
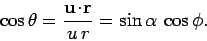 |
(1671) |
It is easily seen that
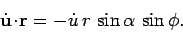 |
(1672) |
A little vector algebra shows that
![\begin{displaymath}[{\bf r}\times({\bf r}_u\times \dot{\bf u})]^2 =
-({\bf r}\!...
...^2/c^2)
+\dot{u}^2 r^4 (1-{\bf r}\!\cdot\!{\bf u}/r c)^2,
\end{displaymath}](img3367.png) |
(1673) |
giving
![\begin{displaymath}[{\bf r}\times({\bf r}_u\times \dot{\bf u})]^2 =
\dot{u}^2 ...
...t(
1-\frac{u^2}{c^2}\right) \tan^2 \phi \cos^2\theta\right].
\end{displaymath}](img3368.png) |
(1674) |
Making use of Eq. (1659), we obtain
![\begin{displaymath}
\frac{d P(t')}{d{\mit\Omega}} = \frac{e^2 \dot{u}^2}{16\pi...
...1-u^2/c^2)\tan^2\phi \cos^2\theta}
{[1-(u/c) \cos\theta]^5}.
\end{displaymath}](img3369.png) |
(1675) |
It is convenient to write this result in terms of the angles
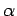 and
and  , instead of
, instead of 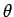 and
and  . After a
little algebra we obtain
. After a
little algebra we obtain
![\begin{displaymath}
\frac{d P(t')}{d{\mit\Omega}} = \frac{e^2 \dot{u}^2}{16\pi...
...-\sin\alpha \cos\phi]^2}
{[1-(u/c) \sin\alpha \cos\phi]^5}.
\end{displaymath}](img3370.png) |
(1676) |
Let us consider the radiation pattern emitted in the plane of the
orbit: i.e., 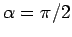 , with
, with
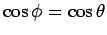 . It is easily seen that
. It is easily seen that
![\begin{displaymath}
\frac{d P(t')}{d{\mit\Omega}} = \frac{e^2 \dot{u}^2}{16\pi...
... c^3}
\frac{[(u/c) - \cos\theta]^2}{[1-(u/c) \cos\theta]^5}.
\end{displaymath}](img3373.png) |
(1677) |
In the non-relativistic limit, the radiation pattern has a 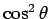 dependence. Thus, the pattern is like
that of dipole radiation where the axis is
aligned along the instantaneous direction of acceleration. As the
charge becomes more relativistic, the radiation lobe in the forward
direction
(i.e.,
dependence. Thus, the pattern is like
that of dipole radiation where the axis is
aligned along the instantaneous direction of acceleration. As the
charge becomes more relativistic, the radiation lobe in the forward
direction
(i.e.,
 )
becomes more more focused and more intense. Likewise, the
radiation lobe in the backward direction
(i.e.,
)
becomes more more focused and more intense. Likewise, the
radiation lobe in the backward direction
(i.e.,
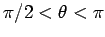 ) becomes more diffuse.
The radiation pattern has zero intensity at the angles
) becomes more diffuse.
The radiation pattern has zero intensity at the angles
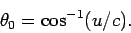 |
(1678) |
These angles demark the boundaries between the two radiation
lobes.
In the non-relativistic limit,
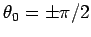 , so the two lobes are
of equal angular extents. In the highly relativistic limit,
, so the two lobes are
of equal angular extents. In the highly relativistic limit,
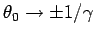 , so the forward
lobe becomes highly concentrated about the forward direction (
, so the forward
lobe becomes highly concentrated about the forward direction ( ).
In the latter limit, Eq. (1677) reduces to
).
In the latter limit, Eq. (1677) reduces to
![\begin{displaymath}
\frac{dP(t')}{d{\mit\Omega}} \simeq \frac{e^2 \dot{u}^2}{2...
...^6 \frac{[1-(\gamma \theta)^2]^2}{[1+(\gamma \theta)^2]^5}.
\end{displaymath}](img3379.png) |
(1679) |
Thus, the radiation emitted by a highly relativistic charge is focused into
an intense beam, of angular extent 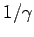 , pointing in the instantaneous
direction of motion. The maximum intensity of the beam scales like
, pointing in the instantaneous
direction of motion. The maximum intensity of the beam scales like 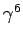 .
.
Integration of Eq. (1676) over all solid angle (using
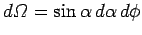 ) yields
) yields
 |
(1680) |
which agrees with Eq. (1649), provided that
 . This expression can also be written
. This expression can also be written
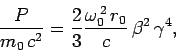 |
(1681) |
where
 meters
is the classical electron radius,
meters
is the classical electron radius, 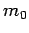 is the rest mass of the charge,
and
is the rest mass of the charge,
and 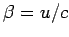 . If the circular motion takes place in an orbit of radius
. If the circular motion takes place in an orbit of radius
 , perpendicular to a magnetic field
, perpendicular to a magnetic field 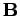 , then
, then 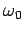 satisfies
satisfies
 . Thus, the radiated power is
. Thus, the radiated power is
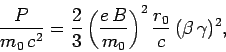 |
(1682) |
and the radiated energy
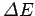 per revolution is
per revolution is
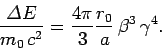 |
(1683) |
Let us consider the frequency distribution of the emitted radiation
in the highly relativistic limit. Suppose, for the sake of
simplicity, that the observation point lies in the plane of
the orbit (i.e., 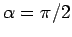 ). Since the radiation emitted
by the charge is beamed very strongly in the
charge's instantaneous direction
of motion, a fixed observer is only going to see radiation (at some
later time)
when this direction points almost directly towards the point of observation.
This occurs once every rotation period, when
). Since the radiation emitted
by the charge is beamed very strongly in the
charge's instantaneous direction
of motion, a fixed observer is only going to see radiation (at some
later time)
when this direction points almost directly towards the point of observation.
This occurs once every rotation period, when 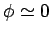 , assuming that
, assuming that
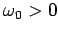 . Note that the point of observation is located many
orbit radii away from the centre of the orbit along the positive
. Note that the point of observation is located many
orbit radii away from the centre of the orbit along the positive
 -axis. Thus, our observer sees short periodic
pulses of radiation
from the charge. The repetition
frequency of the pulses (in radians per second)
is
-axis. Thus, our observer sees short periodic
pulses of radiation
from the charge. The repetition
frequency of the pulses (in radians per second)
is 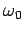 . Let us calculate the duration of each pulse. Since the
radiation emitted by the charge is focused into a narrow beam of
angular extent
. Let us calculate the duration of each pulse. Since the
radiation emitted by the charge is focused into a narrow beam of
angular extent
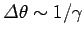 , our observer only sees
radiation from the charge when
, our observer only sees
radiation from the charge when
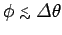 . Thus,
the observed pulse is emitted during a time interval
. Thus,
the observed pulse is emitted during a time interval
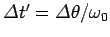 . However,
the pulse is received in a somewhat shorter time interval
. However,
the pulse is received in a somewhat shorter time interval
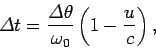 |
(1684) |
because the charge is slightly closer to the point of observation at the
end of the pulse than at the beginning. The above equation
reduces to
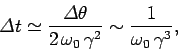 |
(1685) |
since 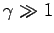 and
and
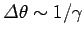 .
The width
.
The width
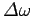 of the pulse in frequency space obeys
of the pulse in frequency space obeys
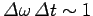 . Hence,
. Hence,
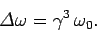 |
(1686) |
In other words, the emitted frequency spectrum contains harmonics
up to 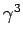 times that of the cyclotron frequency,
times that of the cyclotron frequency, 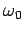 .
.



Next: About this document ...
Up: Relativity and electromagnetism
Previous: Angular distribution of radiation
Richard Fitzpatrick
2006-02-02
![]() with constant
angular velocity
with constant
angular velocity ![]() . Suppose that the orbit lies in the
. Suppose that the orbit lies in the ![]() -
-![]() plane. The radius vector pointing from the centre of the orbit
to the retarded position of the charge is defined
plane. The radius vector pointing from the centre of the orbit
to the retarded position of the charge is defined
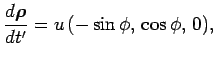
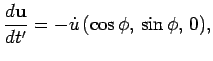
![\begin{displaymath}[{\bf r}\times({\bf r}_u\times \dot{\bf u})]^2 =
\dot{u}^2 ...
...t(
1-\frac{u^2}{c^2}\right) \tan^2 \phi \cos^2\theta\right].
\end{displaymath}](img3368.png)
![\begin{displaymath}
\frac{d P(t')}{d{\mit\Omega}} = \frac{e^2 \dot{u}^2}{16\pi...
...1-u^2/c^2)\tan^2\phi \cos^2\theta}
{[1-(u/c) \cos\theta]^5}.
\end{displaymath}](img3369.png)
![]() , with
, with
![]() . It is easily seen that
. It is easily seen that
![\begin{displaymath}
\frac{dP(t')}{d{\mit\Omega}} \simeq \frac{e^2 \dot{u}^2}{2...
...^6 \frac{[1-(\gamma \theta)^2]^2}{[1+(\gamma \theta)^2]^5}.
\end{displaymath}](img3379.png)
![]() ) yields
) yields

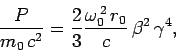
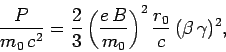
![]() ). Since the radiation emitted
by the charge is beamed very strongly in the
charge's instantaneous direction
of motion, a fixed observer is only going to see radiation (at some
later time)
when this direction points almost directly towards the point of observation.
This occurs once every rotation period, when
). Since the radiation emitted
by the charge is beamed very strongly in the
charge's instantaneous direction
of motion, a fixed observer is only going to see radiation (at some
later time)
when this direction points almost directly towards the point of observation.
This occurs once every rotation period, when ![]() , assuming that
, assuming that
![]() . Note that the point of observation is located many
orbit radii away from the centre of the orbit along the positive
. Note that the point of observation is located many
orbit radii away from the centre of the orbit along the positive
![]() -axis. Thus, our observer sees short periodic
pulses of radiation
from the charge. The repetition
frequency of the pulses (in radians per second)
is
-axis. Thus, our observer sees short periodic
pulses of radiation
from the charge. The repetition
frequency of the pulses (in radians per second)
is ![]() . Let us calculate the duration of each pulse. Since the
radiation emitted by the charge is focused into a narrow beam of
angular extent
. Let us calculate the duration of each pulse. Since the
radiation emitted by the charge is focused into a narrow beam of
angular extent
![]() , our observer only sees
radiation from the charge when
, our observer only sees
radiation from the charge when
![]() . Thus,
the observed pulse is emitted during a time interval
. Thus,
the observed pulse is emitted during a time interval
![]() . However,
the pulse is received in a somewhat shorter time interval
. However,
the pulse is received in a somewhat shorter time interval