Next: Principal axes of rotation Up: Rigid body rotation Previous: Moment of inertia tensor
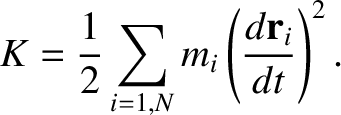 |
(8.14) |
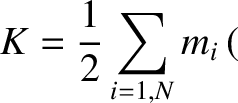 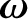 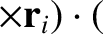 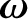 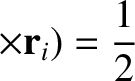 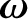 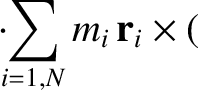 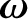 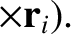 |
(8.15) |
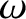
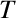 is the row vector of the Cartesian components
is the row vector of the Cartesian components
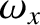 ,
, 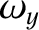 ,
, 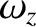 , which is, of course, the transpose
(denoted
, which is, of course, the transpose
(denoted 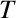 ) of the column vector
) of the column vector
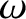 .
When written in component form, Equation (8.17) yields
.
When written in component form, Equation (8.17) yields