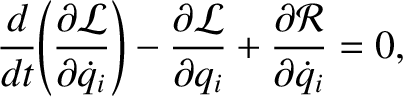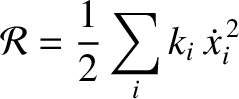Next: Rigid body rotation Up: Lagrangian mechanics Previous: Generalized momenta
 rotates with constant angular velocity
rotates with constant angular velocity  about
its mid-point
about
its mid-point  . A particle
. A particle  is attached to it by equal-length strings
is attached to it by equal-length strings 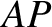 ,
, 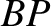 .
If
.
If  is the inclination of the plane
is the inclination of the plane 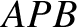 to the vertical, prove that
to the vertical, prove that
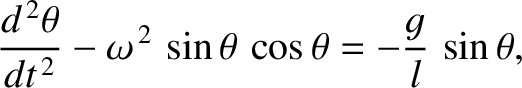
 . Deduce the condition that the vertical position of
. Deduce the condition that the vertical position of  should be stable.
should be stable.
 ,
and bobs of equal mass,
,
and bobs of equal mass,  , and are confined to move in the
same vertical plane.
Let
, and are confined to move in the
same vertical plane.
Let  and
and 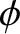 —the angles that the upper and
lower pendula make with the downward vertical (respectively)—be the
generalized coordinates. Demonstrate that Lagrange's equations of motion for the system
are
—the angles that the upper and
lower pendula make with the downward vertical (respectively)—be the
generalized coordinates. Demonstrate that Lagrange's equations of motion for the system
are
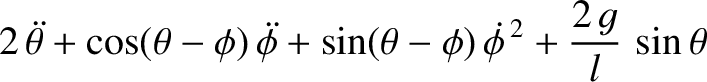 |
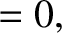 |
|
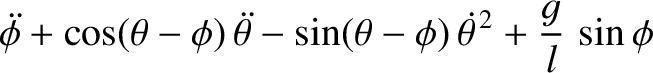 |
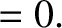 |
 attached to a light elastic string of stiffness
attached to a light elastic string of stiffness 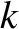 and unstreatched
length
and unstreatched
length  . Let
. Let  be the extension of the string, and
be the extension of the string, and  the angle that the
string makes with the downward vertical. Assume that any motion is confined to a vertical plane.
Demonstrate that Lagrange's equations of motion for the system are
the angle that the
string makes with the downward vertical. Assume that any motion is confined to a vertical plane.
Demonstrate that Lagrange's equations of motion for the system are
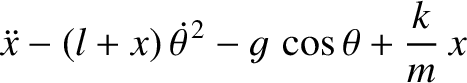 |
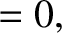 |
|
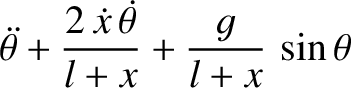 |
 |
 and radius
and radius 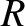 rolls without slipping down a plane inclined at an angle
rolls without slipping down a plane inclined at an angle 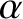 to the horizontal.
The disk has a short weightless axle of negligible radius. From this axle is suspended a simple pendulum
of length
to the horizontal.
The disk has a short weightless axle of negligible radius. From this axle is suspended a simple pendulum
of length  whose bob is of mass
whose bob is of mass  . Assume that the motion of the pendulum takes place in the
plane of the disk. Let
. Assume that the motion of the pendulum takes place in the
plane of the disk. Let 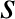 be the displacement of the center of mass of the disk down the slope, and let
be the displacement of the center of mass of the disk down the slope, and let
 be the angle subtended between the pendulum and the downward vertical.
Demonstrate that Lagrange's equations of motion for the system are
be the angle subtended between the pendulum and the downward vertical.
Demonstrate that Lagrange's equations of motion for the system are
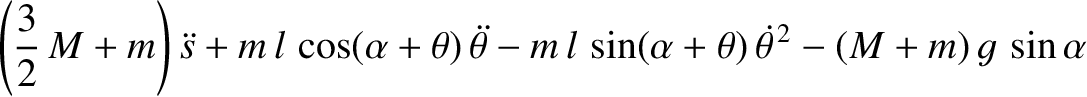 |
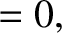 |
|
 |
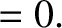 |
![\includegraphics[height=1.75in]{Chapter06/fig6_01.eps}](img1484.png)
 is rotated in a vertical plane about a point
is rotated in a vertical plane about a point 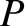 on its
circumference at the constant angular velocity
on its
circumference at the constant angular velocity 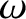 . A bead of
mass
. A bead of
mass  slides without friction on the hoop. Let the generalized coordinate be the angle
slides without friction on the hoop. Let the generalized coordinate be the angle  shown in the diagram. Here,
shown in the diagram. Here,  is a horizontal Cartesian coordinate,
is a horizontal Cartesian coordinate,
 a vertical Cartesian coordinate, and
a vertical Cartesian coordinate, and  the center of the hoop. Demonstrate that the equation
of motion of the system is
the center of the hoop. Demonstrate that the equation
of motion of the system is
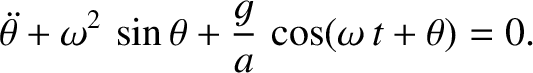
![$\displaystyle K = \frac{1}{2}\left[{\cal I}_\perp\,\skew{5}\dot{\theta}^{\,2} +...
...hi}\,\skew{5}\dot{\psi} + {\cal I}_\parallel\,\skew{5}\dot{\psi}^{\,2}\right],
$](img1466.png)
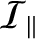 is the moment of inertia about the symmetry axis,
is the moment of inertia about the symmetry axis,
 is the moment of inertia about an axis perpendicular to the symmetry axis, and
is the moment of inertia about an axis perpendicular to the symmetry axis, and  ,
, 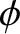 ,
, 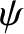 are the three Euler angles. (See Chapter 8.)
Suppose that the object is rotating freely.
Find the momenta conjugate to the Euler angles. Which of these
momenta are conserved? Find Lagrange's equations of motion for the
system. Demonstrate that if the system is precessing steadily (which
implies that
are the three Euler angles. (See Chapter 8.)
Suppose that the object is rotating freely.
Find the momenta conjugate to the Euler angles. Which of these
momenta are conserved? Find Lagrange's equations of motion for the
system. Demonstrate that if the system is precessing steadily (which
implies that  ,
,
 , and
, and
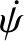 are constants) then
are constants) then
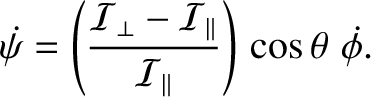
 |
 |
|
 |
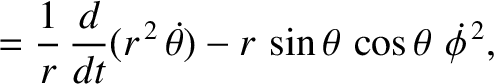 |
|
 |
 |
 . Suppose that the particle is
projected with velocity
. Suppose that the particle is
projected with velocity 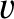 along the horizontal great circle.
Demonstrate that the particle subsequently falls a vertical height
along the horizontal great circle.
Demonstrate that the particle subsequently falls a vertical height
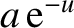 ,
where
,
where
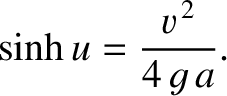
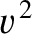 is large compared to
is large compared to  then this height becomes approximately
then this height becomes approximately
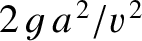 . (From Lamb 1923.)
. (From Lamb 1923.)
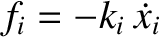 , where the
, where the 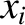 are Cartesian coordinates, and the
are Cartesian coordinates, and the 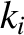 are all positive. Demonstrate that
the dissipative forces can be incorporated into the Lagrangian formalism
provided that Lagrange's equations of motion are modified to read
are all positive. Demonstrate that
the dissipative forces can be incorporated into the Lagrangian formalism
provided that Lagrange's equations of motion are modified to read