Next: Orbits in central force Up: Keplerian orbits Previous: Binary star systems
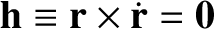 , then the particle's trajectory lies
on a fixed straight line that passes through the origin. [Hint: Show that
, then the particle's trajectory lies
on a fixed straight line that passes through the origin. [Hint: Show that
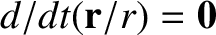 .]
.]
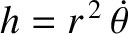 is the magnitude of the angular momentum (per unit mass)
vector
is the magnitude of the angular momentum (per unit mass)
vector
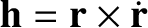 . Here,
. Here,  and
and  are plane polar coordinates.
are plane polar coordinates.
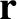 be the planet's position vector, relative to the Sun, and
let
be the planet's position vector, relative to the Sun, and
let
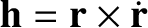 be its angular momentum per unit mass. Demonstrate that the so-called eccentricity vector,
be its angular momentum per unit mass. Demonstrate that the so-called eccentricity vector,
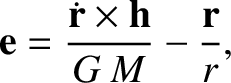
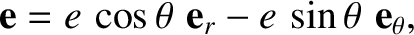
 is the solar mass,
is the solar mass,  the orbital eccentricity, and
the orbital eccentricity, and  ,
,  are plane polar coordinates in the orbital plane (with the perihelion corresponding to
are plane polar coordinates in the orbital plane (with the perihelion corresponding to 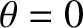 ). Hence, show that
). Hence, show that  is a constant vector, of length
is a constant vector, of length  , that is directed from the Sun toward the
perihelion point.
, that is directed from the Sun toward the
perihelion point.
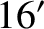 ), the Earth's mean apparent radius seen from the Moon (
), the Earth's mean apparent radius seen from the Moon (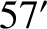 ),
and the mean number of lunar revolutions in a year (
),
and the mean number of lunar revolutions in a year (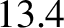 ), show that the ratio of the Sun's mean density to that of the Earth
is
), show that the ratio of the Sun's mean density to that of the Earth
is 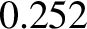 . (From Lamb 1923.)
. (From Lamb 1923.)
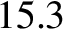 times the
mean radius of the planet. The Moon has an orbital period of 27 d. 7 h. 43 m. and a mean orbital radius that is
times the
mean radius of the planet. The Moon has an orbital period of 27 d. 7 h. 43 m. and a mean orbital radius that is 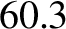 times the Earth's
mean radius. Show that the ratio of Jupiter's mean density to that of the Earth is
times the Earth's
mean radius. Show that the ratio of Jupiter's mean density to that of the Earth is 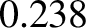 . (From Lamb 1923.)
. (From Lamb 1923.)
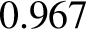 and a perihelion
distance of 55,000,000 miles. Find the orbital period and the comet's speed at
perihelion and aphelion.
and a perihelion
distance of 55,000,000 miles. Find the orbital period and the comet's speed at
perihelion and aphelion.
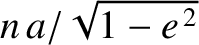 at right angles to the radius vector, and
a velocity
at right angles to the radius vector, and
a velocity
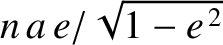 at right angles to the major axis. Here,
at right angles to the major axis. Here, 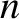 is the mean orbital angular
velocity,
is the mean orbital angular
velocity,  the major radius, and
the major radius, and  the eccentricity. (From Lamb 1923.)
the eccentricity. (From Lamb 1923.)
![$e\,h/[r_p\,(1+e)]$](img885.png) . Here,
. Here, 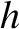 is the angular momentum per unit mass,
is the angular momentum per unit mass,  the orbital eccentricity, and
the orbital eccentricity, and 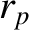 the
perihelion distance.
the
perihelion distance.
 astronomical units from the Sun,
traveling at a speed that is
astronomical units from the Sun,
traveling at a speed that is 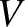 times the Earth's mean orbital speed. Show that the orbit of the
comet is hyperbolic, parabolic, or elliptical, depending on whether the quantity
times the Earth's mean orbital speed. Show that the orbit of the
comet is hyperbolic, parabolic, or elliptical, depending on whether the quantity
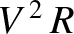 is
greater than, equal to, or less than 2, respectively. (Modified from Fowles and Cassiday 2005.)
is
greater than, equal to, or less than 2, respectively. (Modified from Fowles and Cassiday 2005.)
 and
eccentricity
and
eccentricity  about the Sun. Suppose that the eccentricity of the orbit is small
(i.e.,
about the Sun. Suppose that the eccentricity of the orbit is small
(i.e., 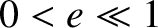 ), as is indeed the case for all of the planets. Demonstrate that, to first order in
), as is indeed the case for all of the planets. Demonstrate that, to first order in  , the orbit can be approximated as a circle whose center is shifted a distance
, the orbit can be approximated as a circle whose center is shifted a distance 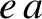 from
the Sun, and that the planet's angular motion appears uniform when
viewed from a point (called the equant) that is shifted a distance
from
the Sun, and that the planet's angular motion appears uniform when
viewed from a point (called the equant) that is shifted a distance
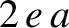 from the Sun, in the same direction as the center of the circle.
[This theorem is the
basis of Ptolemy's model of planetary motion (Evans 1998).]
from the Sun, in the same direction as the center of the circle.
[This theorem is the
basis of Ptolemy's model of planetary motion (Evans 1998).]
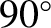 , starting at the perihelion point? How long does it take starting at the aphelion point? The period and eccentricity of the Earth's orbit are
, starting at the perihelion point? How long does it take starting at the aphelion point? The period and eccentricity of the Earth's orbit are 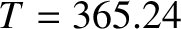 days, and
days, and 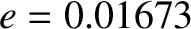 , respectively.
, respectively.
 is the Sun's ecliptic longitude, measured from the perigee (the point of closest approach
to the Earth), show that the Sun's apparent diameter is given by
is the Sun's ecliptic longitude, measured from the perigee (the point of closest approach
to the Earth), show that the Sun's apparent diameter is given by
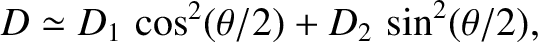
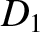 and
and 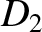 are the greatest and least values of
are the greatest and least values of 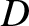 . (From Lamb 1923.)
. (From Lamb 1923.)
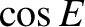 |
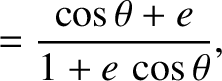 |
|
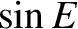 |
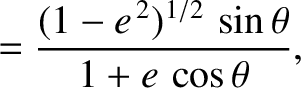 |
|
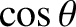 |
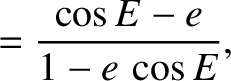 |
|
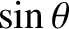 |
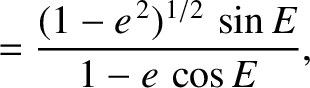 |
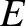 ,
,  , and
, and  are the elliptic anomaly, the true anomaly, and the eccentricity, respectively.
are the elliptic anomaly, the true anomaly, and the eccentricity, respectively.
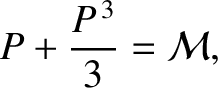
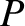 is the parabolic anomaly, and
is the parabolic anomaly, and
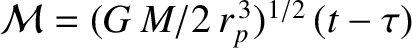 is termed the
parabolic mean anomaly. Here,
is termed the
parabolic mean anomaly. Here,  is the solar mass,
is the solar mass, 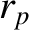 the perihelion distance, and
the perihelion distance, and 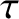 the
time of perihelion passage. Demonstrate that the preceding equation has the analytic solution
the
time of perihelion passage. Demonstrate that the preceding equation has the analytic solution
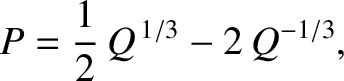
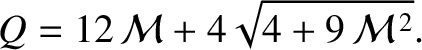
 and
and  be Cartesian coordinates in the
orbital plane, such that
be Cartesian coordinates in the
orbital plane, such that 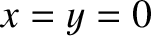 corresponds to the Sun, and the
corresponds to the Sun, and the  -axis is
parallel to the orbital major axis. Demonstrate that
-axis is
parallel to the orbital major axis. Demonstrate that
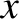 |
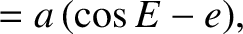 |
|
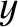 |
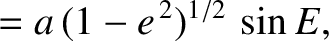 |
 is the orbital major radius,
is the orbital major radius,  the eccentricity, and
the eccentricity, and 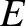 the eccentric anomaly.
the eccentric anomaly.
 and
and  be Cartesian coordinates in the
orbital plane, such that
be Cartesian coordinates in the
orbital plane, such that 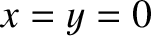 corresponds to the Sun, and the
corresponds to the Sun, and the  -axis is
parallel to the orbital symmetry axis. Demonstrate that
-axis is
parallel to the orbital symmetry axis. Demonstrate that
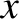 |
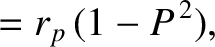 |
|
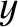 |
 |
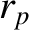 is the perihelion distance, and
is the perihelion distance, and  the parabolic anomaly.
the parabolic anomaly.
 and
and  be Cartesian coordinates in the
orbital plane, such that
be Cartesian coordinates in the
orbital plane, such that 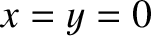 corresponds to the Sun, and the
corresponds to the Sun, and the  -axis is
parallel to the orbital symmetry axis. Demonstrate that
-axis is
parallel to the orbital symmetry axis. Demonstrate that
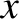 |
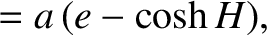 |
|
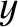 |
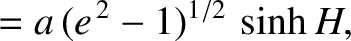 |
 is the orbital major radius,
is the orbital major radius,  the eccentricity, and
the eccentricity, and 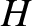 the hyperbolic anomaly.
the hyperbolic anomaly.
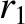 and
and 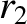 are the radial distances from the Sun of two neighboring points,
are the radial distances from the Sun of two neighboring points, 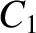 and
and  , on the orbit, and
if
, on the orbit, and
if 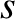 is the length of the straight line joining these two points, prove that the time,
is the length of the straight line joining these two points, prove that the time, 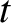 , required for the comet to
move from
, required for the comet to
move from 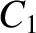 to
to  is
is
![$\displaystyle {\mit\Delta} t =\frac{T}{2\pi}\left[ (\eta -\sin\eta) -(\xi - \sin\xi)\right],
$](img915.png)
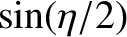 |
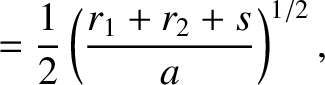 |
|
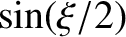 |
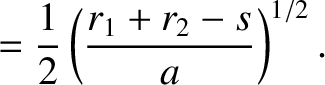 |
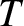 and
and  are the period and the major radius of the orbit, respectively.
are the period and the major radius of the orbit, respectively.
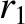 and
and 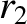 are the radial distances from the Sun of two neighboring points,
are the radial distances from the Sun of two neighboring points, 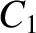 and
and  , on the orbit, and
if
, on the orbit, and
if 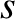 is the length of the straight line joining these two points, prove that the time required for the comet to
move from
is the length of the straight line joining these two points, prove that the time required for the comet to
move from 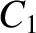 to
to  is
is
![$\displaystyle {\mit\Delta} t = \frac{T}{12\pi}\left[\left(\frac{r_1+r_2+s}{a}\right)^{3/2}-\left(\frac{r_1+r_2-s}{a}\right)^{3/2}\right],
$](img920.png)
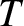 and
and  are the period and the major radius of the Earth's orbit, respectively.
are the period and the major radius of the Earth's orbit, respectively.
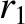 and
and 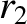 are the radial distances from the Sun of two neighboring points,
are the radial distances from the Sun of two neighboring points, 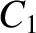 and
and  , on the orbit, and
if
, on the orbit, and
if 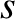 is the length of the straight line joining these two points, prove that the time,
is the length of the straight line joining these two points, prove that the time, 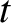 , required for the comet to
move from
, required for the comet to
move from 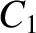 to
to  is
is
![$\displaystyle {\mit\Delta} t =\frac{T}{2\pi}\left[ (\sinh\eta-\eta) -(\sinh\xi-\xi)\right],
$](img921.png)
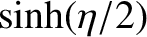 |
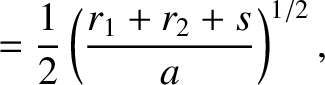 |
|
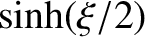 |
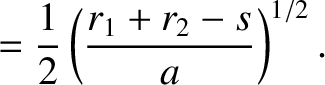 |
 is major radius of the orbit, and
is major radius of the orbit, and  is the period of an elliptical orbit with the same major radius. (From Smart 1951.)
is the period of an elliptical orbit with the same major radius. (From Smart 1951.)
 , show that the points
at which the comet intersects the Earth's orbit are given by
, show that the points
at which the comet intersects the Earth's orbit are given by
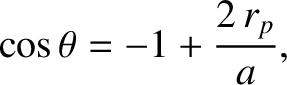
 is the perihelion distance of the comet, defined at
is the perihelion distance of the comet, defined at 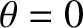 .
Demonstrate that the time interval that the comet remains inside the Earth's orbit is the
faction
.
Demonstrate that the time interval that the comet remains inside the Earth's orbit is the
faction
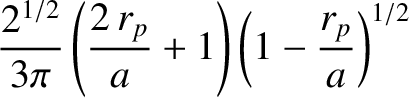
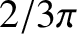 year, or
about 11 weeks.
year, or
about 11 weeks.
 , lying in the ecliptic plane, whose
least distance from the Sun is
, lying in the ecliptic plane, whose
least distance from the Sun is 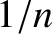 times the radius of the Earth's orbit (which is approximated as a circle).
Prove that the time that the comet remains within the Earth's orbit is
times the radius of the Earth's orbit (which is approximated as a circle).
Prove that the time that the comet remains within the Earth's orbit is
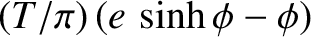 , where
, where
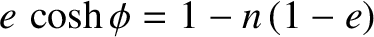 , and
, and 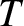 is the periodic time of a planet describing an elliptic
orbit whose major radius is equal to that of the hyperbolic orbit. (From Smart 1951.)
is the periodic time of a planet describing an elliptic
orbit whose major radius is equal to that of the hyperbolic orbit. (From Smart 1951.)
 is defined as the the distance of closest approach
in the absence of any gravitational attraction between the comet and the Sun.
Demonstrate that
is defined as the the distance of closest approach
in the absence of any gravitational attraction between the comet and the Sun.
Demonstrate that
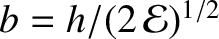 , where
, where
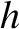 is the comet's angular momentum per unit mass, and
is the comet's angular momentum per unit mass, and  its energy per unit mass. Show that the relationship between the impact parameter,
its energy per unit mass. Show that the relationship between the impact parameter, 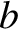 , and the
true distance of closest approach,
, and the
true distance of closest approach, 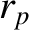 , is
, is
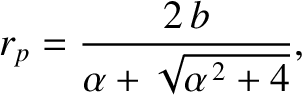
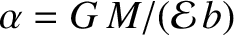 , and
, and  is the solar mass. Hence, deduce that if the comet is
to avoid hitting the Sun then
is the solar mass. Hence, deduce that if the comet is
to avoid hitting the Sun then
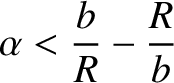
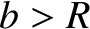 ), where
), where  is the solar radius.
is the solar radius.
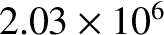 miles, and that the total mass of the system is
miles, and that the total mass of the system is
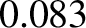 that of the Sun. The mean distance of the Earth from the Sun is
that of the Sun. The mean distance of the Earth from the Sun is 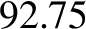 million miles. (From Lamb 1923.)
million miles. (From Lamb 1923.)
 |
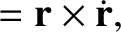 |
|
 |
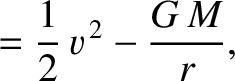 |
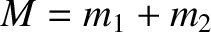 and
and
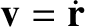 , are integrals of the the reduced equation of motion, (4.110) (in other words,
, are integrals of the the reduced equation of motion, (4.110) (in other words, 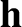 and
and  are constants of the motion). Demonstrate that, in the center of mass frame, the net angular momentum and energy of the
system are
are constants of the motion). Demonstrate that, in the center of mass frame, the net angular momentum and energy of the
system are
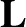 |
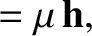 |
|
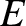 |
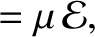 |
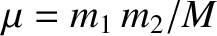 is the reduced mass.
is the reduced mass.