Plane polar coordinates
Figure 4.1:
Plane polar coordinates.
|
|
We can determine the instantaneous position of our planet in the
 -
- plane in terms of standard Cartesian coordinates,
plane in terms of standard Cartesian coordinates,  ,
,  ,
or plane polar coordinates,
,
or plane polar coordinates,  ,
,  , as illustrated in Figure 4.1. Here,
, as illustrated in Figure 4.1. Here,
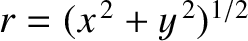 and
and
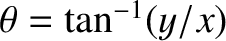 .
It is helpful to define two unit vectors,
.
It is helpful to define two unit vectors,
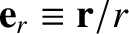 and
and
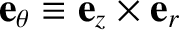 , at the
instantaneous position of the planet. The first always points radially away from the origin,
whereas the second is normal to the first, in the direction of increasing
, at the
instantaneous position of the planet. The first always points radially away from the origin,
whereas the second is normal to the first, in the direction of increasing  . As is easily demonstrated, the Cartesian components of
. As is easily demonstrated, the Cartesian components of
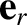 and
and
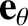 are
are
respectively.
We can write the position vector of our planet as
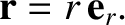 |
(4.10) |
Thus, the planet's velocity becomes
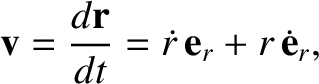 |
(4.11) |
where
 is shorthand for
is shorthand for 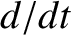 . Note that
. Note that 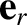 has a non-zero time derivative (unlike a Cartesian unit vector) because its
direction changes as the planet moves around. As is easily demonstrated,
by differentiating Equation (4.8) with respect to time,
has a non-zero time derivative (unlike a Cartesian unit vector) because its
direction changes as the planet moves around. As is easily demonstrated,
by differentiating Equation (4.8) with respect to time,
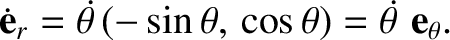 |
(4.12) |
Thus,
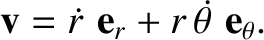 |
(4.13) |
The planet's acceleration is written
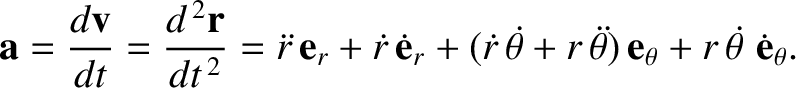 |
(4.14) |
Again,
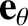 has a nonzero time derivative because its
direction changes as the planet moves around.
Differentiation of Equation (4.9) with respect to time yields
has a nonzero time derivative because its
direction changes as the planet moves around.
Differentiation of Equation (4.9) with respect to time yields
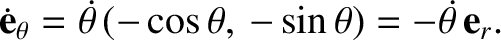 |
(4.15) |
Hence,
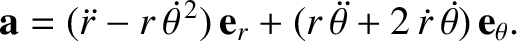 |
(4.16) |
It follows that the equation of motion of our planet, Equation (4.2), can be written
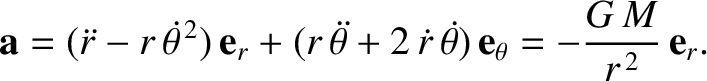 |
(4.17) |
Because 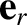 and
and
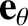 are mutually orthogonal, we can separately equate the coefficients of both, in the preceding equation, to give
a radial equation of motion,
are mutually orthogonal, we can separately equate the coefficients of both, in the preceding equation, to give
a radial equation of motion,
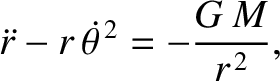 |
(4.18) |
and a tangential equation of motion,
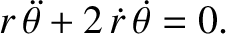 |
(4.19) |
 -
- plane in terms of standard Cartesian coordinates,
plane in terms of standard Cartesian coordinates,  ,
,  ,
or plane polar coordinates,
,
or plane polar coordinates,  ,
,  , as illustrated in Figure 4.1. Here,
, as illustrated in Figure 4.1. Here,
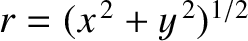 and
and
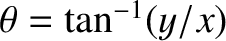 .
It is helpful to define two unit vectors,
.
It is helpful to define two unit vectors,
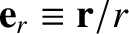 and
and
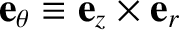 , at the
instantaneous position of the planet. The first always points radially away from the origin,
whereas the second is normal to the first, in the direction of increasing
, at the
instantaneous position of the planet. The first always points radially away from the origin,
whereas the second is normal to the first, in the direction of increasing  . As is easily demonstrated, the Cartesian components of
. As is easily demonstrated, the Cartesian components of
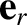 and
and
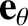 are
are
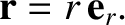
 is shorthand for
is shorthand for 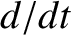 . Note that
. Note that 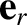 has a non-zero time derivative (unlike a Cartesian unit vector) because its
direction changes as the planet moves around. As is easily demonstrated,
by differentiating Equation (4.8) with respect to time,
has a non-zero time derivative (unlike a Cartesian unit vector) because its
direction changes as the planet moves around. As is easily demonstrated,
by differentiating Equation (4.8) with respect to time,
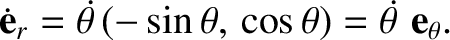
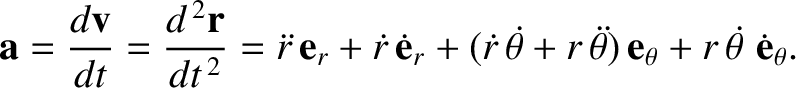
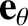 has a nonzero time derivative because its
direction changes as the planet moves around.
Differentiation of Equation (4.9) with respect to time yields
has a nonzero time derivative because its
direction changes as the planet moves around.
Differentiation of Equation (4.9) with respect to time yields
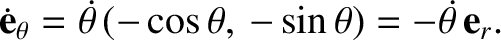
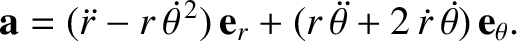
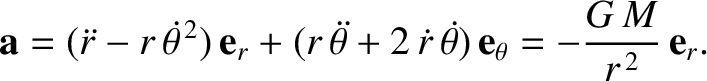
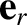 and
and
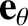 are mutually orthogonal, we can separately equate the coefficients of both, in the preceding equation, to give
a radial equation of motion,
and a tangential equation of motion,
are mutually orthogonal, we can separately equate the coefficients of both, in the preceding equation, to give
a radial equation of motion,
and a tangential equation of motion,