Expansion of planetary disturbing functions
Equations (10.8), (10.9), (H.1), and (H.27)
give
where
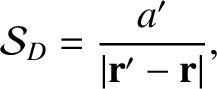 |
(H.38) |
and
In the preceding equations, 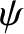 is the angle subtended between the directions of
is the angle subtended between the directions of 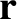 and
and 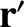 .
.
Now,
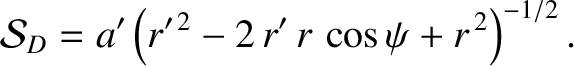 |
(H.41) |
Let
where
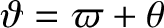 and
and
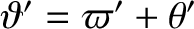 . Here,
. Here,  and
and 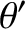 are the
true anomalies of the first and second planets, respectively. We expect
are the
true anomalies of the first and second planets, respectively. We expect  and
and 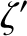 to both be
to both be
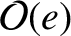 [see Equation (H.54)], and
[see Equation (H.54)], and 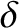 to be
to be
 [see Equation (H.64)]. We can write
[see Equation (H.64)]. We can write
![$\displaystyle {\cal S}_D = (1+\zeta')^{-1}\,\left[1-2\,\tilde{\alpha}\,\cos(\vartheta-\vartheta')+\tilde{\alpha}^2 -2\,\tilde{\alpha}\,\delta\right]^{-1/2},$](img4960.png) |
(H.45) |
where
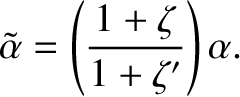 |
(H.46) |
Expanding in  , and retaining terms only up to
, and retaining terms only up to
 ,
we obtain
,
we obtain
![$\displaystyle {\cal S}_D \simeq (1+\zeta')^{-1}\left[F + (\tilde{\alpha}-\alpha...
...c{1}{2}\,(\tilde{\alpha}-\alpha)^2\,D^{\,2}\,F\right]+
\delta\,\alpha\,F^{\,3},$](img4962.png) |
(H.47) |
where
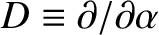 , and
, and
![$\displaystyle F(\alpha,\vartheta-\vartheta') = \frac{1}{[1-2\,\alpha\,\cos(\vartheta-\vartheta')+\alpha^{\,2}]^{1/2}}.$](img4964.png) |
(H.48) |
Hence,
Now,
we can expand 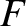 and
and 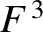 as Fourier series in
as Fourier series in
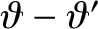 :
where
:
where
![$\displaystyle b_s^{(j)}(\alpha) = \frac{1}{\pi}\int_0^{2\pi}\frac{\cos(j\,\psi)\,d\psi}{[1-2\,\alpha\,\cos\psi+\alpha^{\,2}]^s}.$](img4974.png) |
(H.52) |
Incidentally, the 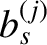 are known as Laplace coefficients.
Thus,
where
are known as Laplace coefficients.
Thus,
where 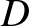 now denotes
now denotes  .
.
Equation (4.87) gives
to
 . Here,
. Here,
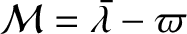 is the first planet's mean anomaly. Obviously, there is an analogous
equation for
is the first planet's mean anomaly. Obviously, there is an analogous
equation for 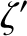 .
Moreover, from Equation (4.86), we have
Hence,
and
Thus, Equations (4.72)–(4.74) yield
where
.
Moreover, from Equation (4.86), we have
Hence,
and
Thus, Equations (4.72)–(4.74) yield
where
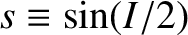 is assumed to be
is assumed to be
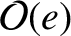 . Here,
. Here, 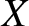 ,
, 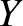 ,
, 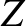 are the Cartesian component of
are the Cartesian component of 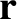 . There are, of course, completely
analogous expressions for the Cartesian components of
. There are, of course, completely
analogous expressions for the Cartesian components of 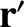 .
.
Now,
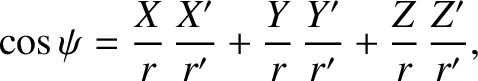 |
(H.62) |
so
It is easily demonstrated that
 represents the value
taken by
represents the value
taken by 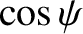 when
when  . Hence, from Equations (H.44) and (H.63),
. Hence, from Equations (H.44) and (H.63),
Now,
![$\displaystyle \cos[ j\,(\vartheta-\vartheta') ]\equiv \cos( j\,\vartheta)\,\cos(j\,\vartheta') + \sin( j\,\vartheta)\,\sin (j\,\vartheta').$](img5017.png) |
(H.65) |
However, from Equation (4.86),
because
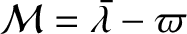 .
Likewise,
Hence, we obtain
.
Likewise,
Hence, we obtain
Equations (H.53), (H.54), (H.64), and
(H.68) yield
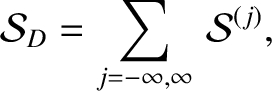 |
(H.69) |
where
Likewise, Equations (H.39), (H.40), (H.54), and (H.63)
give
and
We can distinguish two different types of term that appear in our expansion
of the disturbing functions. Periodic terms vary sinusoidally
in time as our two planets orbit the Sun (i.e., they depend on the mean
ecliptic longitudes,
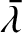 and
and
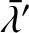 ), whereas secular terms remain constant in time (i.e., they do not depend on
), whereas secular terms remain constant in time (i.e., they do not depend on
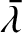 or
or
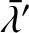 ). We expect the periodic terms to give rise to relatively short-period (i.e., of order a typical orbital period) oscillations in the osculating orbital
elements of our planets. On the other hand, we expect the secular terms to
produce an initially linear increase in these elements with time. Because
such an increase can become significant over a long period of time, even
if the rate of increase is small, it is necessary to evaluate the secular terms
in the disturbing function to higher order than the periodic terms.
Hence, in the following, we shall evaluate periodic terms to
). We expect the periodic terms to give rise to relatively short-period (i.e., of order a typical orbital period) oscillations in the osculating orbital
elements of our planets. On the other hand, we expect the secular terms to
produce an initially linear increase in these elements with time. Because
such an increase can become significant over a long period of time, even
if the rate of increase is small, it is necessary to evaluate the secular terms
in the disturbing function to higher order than the periodic terms.
Hence, in the following, we shall evaluate periodic terms to
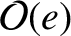 ,
and secular terms to
,
and secular terms to
 .
.
Making use of Equations (H.20), (H.36), and (H.69)–(H.71), as well as the definitions (G.121)–(G.124) (with
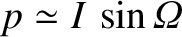 and
and
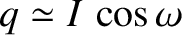 ),
the order by order expansion (in
),
the order by order expansion (in  ) of the first planet's disturbing function becomes
) of the first planet's disturbing function becomes
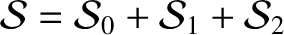 , where
, where
Likewise, the order by order expansion of the second planet's disturbing function becomes
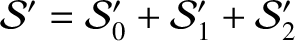 , where
, where
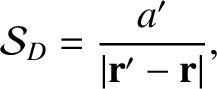
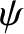 is the angle subtended between the directions of
is the angle subtended between the directions of 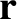 and
and 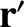 .
.
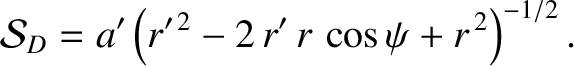
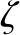
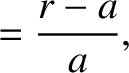
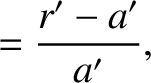

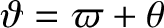 and
and
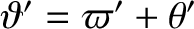 . Here,
. Here,  and
and 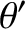 are the
true anomalies of the first and second planets, respectively. We expect
are the
true anomalies of the first and second planets, respectively. We expect  and
and 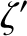 to both be
to both be
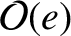 [see Equation (H.54)], and
[see Equation (H.54)], and 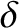 to be
to be
 [see Equation (H.64)]. We can write
[see Equation (H.64)]. We can write
![$\displaystyle {\cal S}_D = (1+\zeta')^{-1}\,\left[1-2\,\tilde{\alpha}\,\cos(\vartheta-\vartheta')+\tilde{\alpha}^2 -2\,\tilde{\alpha}\,\delta\right]^{-1/2},$](img4960.png)
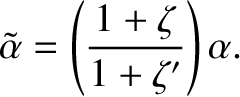
 , and retaining terms only up to
, and retaining terms only up to
 ,
we obtain
,
we obtain
![$\displaystyle {\cal S}_D \simeq (1+\zeta')^{-1}\left[F + (\tilde{\alpha}-\alpha...
...c{1}{2}\,(\tilde{\alpha}-\alpha)^2\,D^{\,2}\,F\right]+
\delta\,\alpha\,F^{\,3},$](img4962.png)
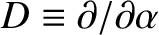 , and
, and
![$\displaystyle F(\alpha,\vartheta-\vartheta') = \frac{1}{[1-2\,\alpha\,\cos(\vartheta-\vartheta')+\alpha^{\,2}]^{1/2}}.$](img4964.png)
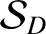
![$\displaystyle \simeq \left[(1-\zeta'+\zeta'^{\,2}) + (\zeta-\zeta'-2\,\zeta\,\z...
...1}{2}(\zeta^{\,2}-2\,\zeta\,\zeta'+\zeta'^{\,2})\,\alpha^{\,2}\,D^{\,2}\right]F$](img4966.png)
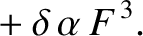
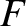 and
and 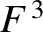 as Fourier series in
as Fourier series in
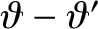 :
:

![$\displaystyle = \frac{1}{2}\sum_{j=-\infty,\infty}b_{1/2}^{(j)}(\alpha)\,\cos[j\,(\vartheta-\vartheta')],$](img4971.png)
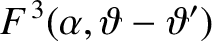
![$\displaystyle = \frac{1}{2}\sum_{j=-\infty,\infty}b_{3/2}^{(j)}(\alpha)\,\cos[j\,(\vartheta-\vartheta')],$](img4973.png)
![$\displaystyle b_s^{(j)}(\alpha) = \frac{1}{\pi}\int_0^{2\pi}\frac{\cos(j\,\psi)\,d\psi}{[1-2\,\alpha\,\cos\psi+\alpha^{\,2}]^s}.$](img4974.png)
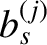 are known as Laplace coefficients.
Thus,
where
are known as Laplace coefficients.
Thus,
where 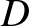 now denotes
now denotes  .
.
 . Here,
. Here,
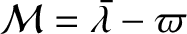 is the first planet's mean anomaly. Obviously, there is an analogous
equation for
is the first planet's mean anomaly. Obviously, there is an analogous
equation for 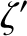 .
Moreover, from Equation (4.86), we have
.
Moreover, from Equation (4.86), we have
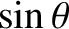

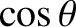
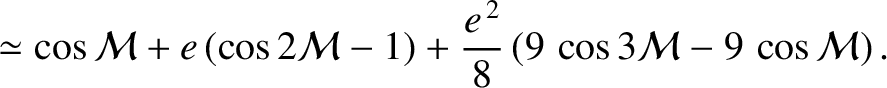
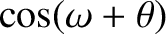

![$\displaystyle \simeq\cos(\omega+{\cal M}) +e\,\left[\cos(\omega+2{\cal M})-\cos\omega\right]$](img4984.png)
![$\displaystyle \phantom{=}+ \frac{e^{\,2}}{8}\left[-8\,\cos(\omega+{\cal M})- \cos(\omega-{\cal M}) + 9\,\cos(\omega+3{\cal M})\right],$](img4985.png)
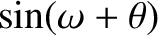
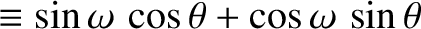
![$\displaystyle \simeq\sin(\omega+{\cal M}) +e\,\left[\sin(\omega+2{\cal M})-\sin\omega\right]$](img4988.png)
![$\displaystyle \phantom{=}+ \frac{e^{\,2}}{8}\left[-8\,\sin(\omega+{\cal M})+ \sin(\omega-{\cal M}) + 9\,\sin(\omega+3{\cal M})\right].$](img4989.png)
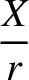
![$\displaystyle \simeq \cos(\omega+{\mit\Omega}+{\cal M}) + e\left[\cos(\omega+{\mit\Omega}+2{\cal M}) - \cos(\omega+{\mit\Omega})\right]$](img4991.png)
![$\displaystyle \phantom{=}+ \frac{e^{\,2}}{8}\left[9\,\cos(\omega+{\mit\Omega}+3...
...os(\omega+{\mit\Omega}-{\cal M}) - 8\,\cos(\omega+{\mit\Omega}+{\cal M})\right]$](img4992.png)
![$\displaystyle \phantom{=}+s^{\,2}\left[\cos(\omega-{\mit\Omega}+{\cal M}) - \cos(\omega+{\mit\Omega}+{\cal M})\right],$](img4993.png)
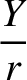
![$\displaystyle \simeq \sin(\omega+{\mit\Omega}+{\cal M}) + e\left[\sin(\omega+{\mit\Omega}+2{\cal M}) - \sin(\omega+{\mit\Omega})\right]$](img4995.png)
![$\displaystyle \phantom{=}+ \frac{e^{\,2}}{8}\left[9\,\sin(\omega+{\mit\Omega}+3...
...in(\omega+{\mit\Omega}-{\cal M}) - 8\,\sin(\omega+{\mit\Omega}+{\cal M})\right]$](img4996.png)
![$\displaystyle \phantom{=}-s^{\,2}\left[\sin(\omega-{\mit\Omega}+{\cal M}) +\sin(\omega+{\mit\Omega}+{\cal M})\right],$](img4997.png)
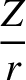
![$\displaystyle \simeq 2\,s\,\sin(\omega+{\cal M}) + 2\,e\,s\left[\sin(\omega+2{\cal M})-\sin\omega)\right],$](img4999.png)
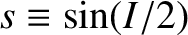 is assumed to be
is assumed to be
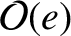 . Here,
. Here, 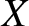 ,
, 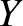 ,
, 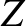 are the Cartesian component of
are the Cartesian component of 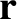 . There are, of course, completely
analogous expressions for the Cartesian components of
. There are, of course, completely
analogous expressions for the Cartesian components of 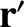 .
.
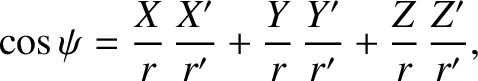
 represents the value
taken by
represents the value
taken by 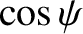 when
when  . Hence, from Equations (H.44) and (H.63),
. Hence, from Equations (H.44) and (H.63),
![$\displaystyle \cos[ j\,(\vartheta-\vartheta') ]\equiv \cos( j\,\vartheta)\,\cos(j\,\vartheta') + \sin( j\,\vartheta)\,\sin (j\,\vartheta').$](img5017.png)
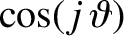
![$\displaystyle \equiv \cos[j\,(\varpi+\theta)]$](img5019.png)
![$\displaystyle \simeq (1-j^{\,2}\,e^{\,2})\,\cos(j\,\skew{5}\bar{\lambda}) + e^{...
...{j^{\,2}}{2}- \frac{5\,j}{8}\right)\cos[(2-j)\,\skew{5}\bar{\lambda}-2\,\varpi]$](img5020.png)
![$\displaystyle \phantom{=}+ e^{\,2}\left(\frac{j^{\,2}}{2} + \frac{5\,j}{8}\right)\cos[(2+j)\,\skew{5}\bar{\lambda}-2\,\varpi]$](img5021.png)
![$\displaystyle \phantom{=}
- j\,e\,\cos[(1-j)\,\skew{5}\bar{\lambda}-\varpi] + j\,e\,\cos[(1+j)\,\skew{5}\bar{\lambda}-\varpi)],$](img5022.png)
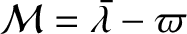 .
Likewise,
.
Likewise,
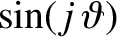
![$\displaystyle \equiv \sin[j\,(\varpi+\theta)]$](img5024.png)
![$\displaystyle \simeq (1-j^{\,2}\,e^{\,2})\,\sin(j\,\skew{5}\bar{\lambda}) + e^{...
...{5\,j}{8}- \frac{j^{\,2}}{2}\right)\sin[(2-j)\,\skew{5}\bar{\lambda}-2\,\varpi]$](img5025.png)
![$\displaystyle \phantom{=}+ e^{\,2}\left(\frac{5\,j}{8} + \frac{j^{\,2}}{2}\right)\sin[(2+j)\,\skew{5}\bar{\lambda}-2\,\varpi]$](img5026.png)
![$\displaystyle \phantom{=}
+ j\,e\,\sin[(1-j)\,\skew{5}\bar{\lambda}-\varpi] + j\,e\,\sin[(1+j)\,\skew{5}\bar{\lambda}-\varpi].$](img5027.png)
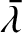 and
and
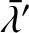 ), whereas secular terms remain constant in time (i.e., they do not depend on
), whereas secular terms remain constant in time (i.e., they do not depend on
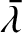 or
or
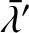 ). We expect the periodic terms to give rise to relatively short-period (i.e., of order a typical orbital period) oscillations in the osculating orbital
elements of our planets. On the other hand, we expect the secular terms to
produce an initially linear increase in these elements with time. Because
such an increase can become significant over a long period of time, even
if the rate of increase is small, it is necessary to evaluate the secular terms
in the disturbing function to higher order than the periodic terms.
Hence, in the following, we shall evaluate periodic terms to
). We expect the periodic terms to give rise to relatively short-period (i.e., of order a typical orbital period) oscillations in the osculating orbital
elements of our planets. On the other hand, we expect the secular terms to
produce an initially linear increase in these elements with time. Because
such an increase can become significant over a long period of time, even
if the rate of increase is small, it is necessary to evaluate the secular terms
in the disturbing function to higher order than the periodic terms.
Hence, in the following, we shall evaluate periodic terms to
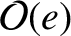 ,
and secular terms to
,
and secular terms to
 .
.
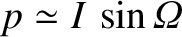 and
and
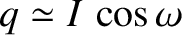 ),
the order by order expansion (in
),
the order by order expansion (in  ) of the first planet's disturbing function becomes
) of the first planet's disturbing function becomes
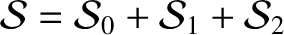 , where
, where
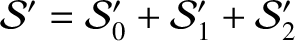 , where
, where