Next: Expansion of planetary disturbing Up: Expansion of orbital evolution Previous: Introduction
 , and
, and  is
is
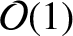 . Thus, because
. Thus, because
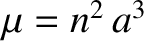 , the Lagrange planetary
equations, Equations (G.125)–(G.130), applied to the first planet, reduce to
where
, the Lagrange planetary
equations, Equations (G.125)–(G.130), applied to the first planet, reduce to
where
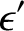 |
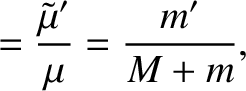 |
(H.8) |
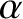 |
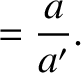 |
(H.9) |
The Sun is much more massive than any planet in the solar system.
It follows that the parameter 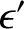 is very small compared to unity.
Expansion of Equations (H.2)–(H.7)
to first order in
is very small compared to unity.
Expansion of Equations (H.2)–(H.7)
to first order in 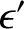 yields
yields
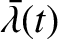 |
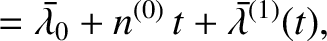 |
(H.10) |
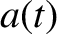 |
![$\displaystyle = a^{(0)}\left[1+\epsilon'\,a^{(1)}(t)\right],$](img4904.png) |
(H.11) |
 |
![$\displaystyle = n^{(0)}\left[1-(3/2)\,\epsilon'\,a^{(1)}(t)\right],$](img4906.png) |
(H.12) |
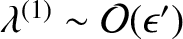 ,
,
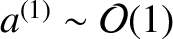 ,
,
![$n^{(0)}=(\mu/[a^{(0)}]^3)^{1/2}$](img2436.png) ,
and
with
,
and
with
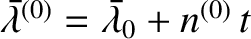 , and
, and
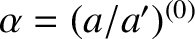 . In the following, for ease of notation,
. In the following, for ease of notation,
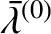 ,
, 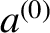 , and
, and 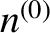 are
written simply as
are
written simply as
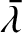 ,
,  , and
, and  , respectively.
, respectively.
According to Table 4.1, the planets in the solar system
all possess orbits whose eccentricities,  , and
inclinations,
, and
inclinations,  (in radians), are small compared to unity, but large compared to
the ratio of any planetary mass to that of the Sun. It follows that
(in radians), are small compared to unity, but large compared to
the ratio of any planetary mass to that of the Sun. It follows that
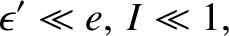 |
(H.19) |
 , we can perform a
secondary expansion in the small parameter
, we can perform a
secondary expansion in the small parameter  . It turns out that
when the normalized disturbing function,
. It turns out that
when the normalized disturbing function,  , is expanded to second order in
, is expanded to second order in  it takes the general form (see Section H.3)
where
it takes the general form (see Section H.3)
where
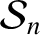 is
is
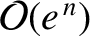 . If we
expand the right-hand sides of Equations (H.13)–(H.18) to
first order in
. If we
expand the right-hand sides of Equations (H.13)–(H.18) to
first order in  then we obtain
Note that
then we obtain
Note that 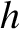 ,
, 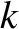 ,
, 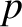 ,
, 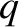 are
are
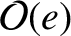 , whereas
, whereas 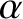 and
and
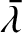 are
are
 .
.
By analogy, writing the second planet's disturbing function as [see Equation (10.9]
where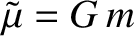 , and
, and  is
is
 , and assuming that
, and assuming that  takes the form
takes the form
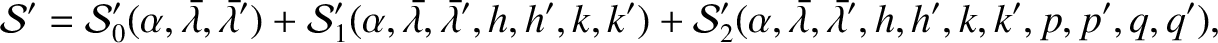 |
(H.28) |
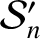 is
is
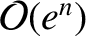 , the Lagrange planetary equations, applied to the second planet, yield
where
, the Lagrange planetary equations, applied to the second planet, yield
where
 |
(H.35) |