The most common set of orbital elements used to parameterize Keplerian orbits consists of the major radius,  ; the mean longitude at epoch,
; the mean longitude at epoch,
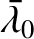 ; the eccentricity,
; the eccentricity,  ;
the inclination (relative to some reference plane),
;
the inclination (relative to some reference plane), 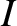 ; the longitude of the perihelion,
; the longitude of the perihelion,
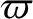 ; and the longitude of the ascending node,
; and the longitude of the ascending node,
 . (See Section 4.12.) The mean orbital angular velocity is
. (See Section 4.12.) The mean orbital angular velocity is
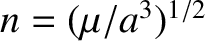 [see Equation (4.117)].
[see Equation (4.117)].
Consider how a particular Lagrange bracket transforms under
a rotation of the coordinate system 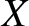 ,
, 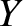 ,
, 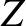 about the
about the 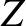 -axis (if we look along the axis).
We can write
-axis (if we look along the axis).
We can write
![$\displaystyle [p,q] = \frac{\partial(X,\dot{X})}{\partial (p,q)}+ \frac{\partial(Y,\dot{Y})}{\partial (p,q)}+ \frac{\partial(Z,\dot{Z})}{\partial (p,q)},$](img4708.png) |
(G.41) |
where
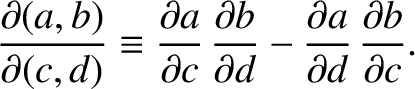 |
(G.42) |
Let the new coordinate system be
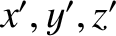 . A rotation about the
. A rotation about the
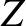 -axis though an angle
-axis though an angle
 brings the ascending node to the
brings the ascending node to the 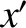 -axis. See Figure 4.6.
The relation between the old and new coordinates is (see Section A.6)
The partial derivatives with respect to
-axis. See Figure 4.6.
The relation between the old and new coordinates is (see Section A.6)
The partial derivatives with respect to 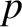 can be written
can be written
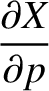 |
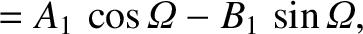 |
(G.46) |
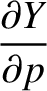 |
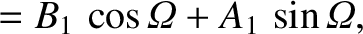 |
(G.47) |
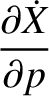 |
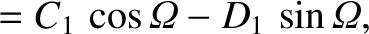 |
(G.48) |
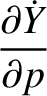 |
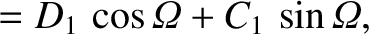 |
(G.49) |
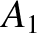 |
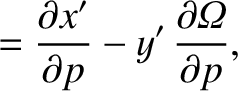 |
(G.50) |
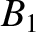 |
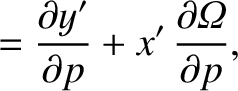 |
(G.51) |
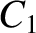 |
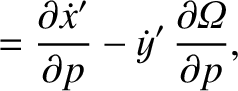 |
(G.52) |
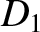 |
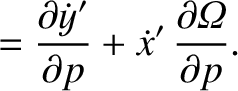 |
(G.53) |
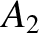 ,
, 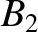 ,
,  , and
, and 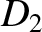 be the equivalent quantities
obtained by replacing
be the equivalent quantities
obtained by replacing 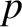 by
by 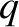 in the preceding equations.
It thus follows that
Hence,
in the preceding equations.
It thus follows that
Hence,
![$\displaystyle [p,q] = A_1\,C_2-A_2\,C_1 + B_1\,D_2-B_2\,D_1+ \frac{\partial(Z,\dot{Z})}{\partial(p,q)}.$](img4735.png) |
(G.56) |
Now,
Similarly,
Let
![$\displaystyle [p,q]' = \frac{\partial(x',\dot{x}')}{\partial (p,q)}+ \frac{\partial(y',\dot{y}')}{\partial (p,q)}+ \frac{\partial(z',\dot{z}')}{\partial (p,q)}.$](img4743.png) |
(G.59) |
Because 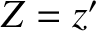 and
and
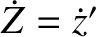 , it follows that
However,
, it follows that
However,
![$\displaystyle x'\,\dot{y}'-y'\,\dot{x}' = h\,\cos\,I = [\mu\,a\,(1-e^{\,2})]^{1/2}\,\cos\,I \equiv {\cal G},$](img4750.png) |
(G.61) |
because the left-hand side is the component of the angular momentum per unit mass parallel to
the 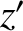 -axis. Of course, this axis is inclined at an angle
-axis. Of course, this axis is inclined at an angle 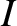 to the
to the  -axis, which is parallel to the angular momentum vector.
Thus, we obtain
-axis, which is parallel to the angular momentum vector.
Thus, we obtain
![$\displaystyle [p,q] = [p,q]' + \frac{\partial({\mit\Omega}, {\cal G})}{\partial (p,q)}.$](img4751.png) |
(G.62) |
Consider a rotation of the coordinate system about the 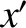 -axis. Let the
new coordinate system be
-axis. Let the
new coordinate system be 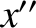 ,
, 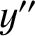 ,
, 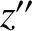 . A rotation through an
angle
. A rotation through an
angle 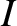 brings the orbit into the
brings the orbit into the 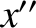 -
-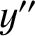 plane. See Figure 4.6.
Let
plane. See Figure 4.6.
Let
![$\displaystyle [p,q]'' = \frac{\partial(x'',\dot{x}'')}{\partial (p,q)}+ \frac{\...
...'',\dot{y}'')}{\partial (p,q)}+ \frac{\partial(z'',\dot{z}'')}{\partial (p,q)}.$](img4752.png) |
(G.63) |
By analogy
with the previous analysis,
![$\displaystyle [p,q]' = [p,q]'' + \frac{\partial(I,y''\,\dot{z}''-z''\,\dot{y}'')}{\partial(p,q)}.$](img4753.png) |
(G.64) |
However, 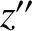 and
and 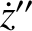 are both zero, because the orbit lies
in the
are both zero, because the orbit lies
in the 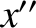 -
-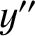 plane. Hence,
plane. Hence,
![$\displaystyle [p,q]'=[p,q]''.$](img4755.png) |
(G.65) |
Consider, finally, a rotation of the coordinate system about the 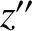 -axis. Let the
final coordinate system be
-axis. Let the
final coordinate system be  ,
,  ,
,  . A rotation through an angle
. A rotation through an angle
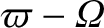 brings the perihelion to the
brings the perihelion to the  -axis. See Figure 4.6.
Let
-axis. See Figure 4.6.
Let
![$\displaystyle [p,q]''' = \frac{\partial(x,\dot{x})}{\partial (p,q)}+ \frac{\partial(y,\dot{y})}{\partial (p,q)}.$](img4757.png) |
(G.66) |
By analogy with the previous analysis,
![$\displaystyle [p,q]'' = [p,q]''' + \frac{\partial(\varpi-{\mit\Omega},x\,\dot{y}-y\,\dot{x})}{\partial (p,q)}.$](img4758.png) |
(G.67) |
However,
![$\displaystyle x\,\dot{y}-y\,\dot{x} = h= [\mu\,a\,(1-e^{\,2})]^{1/2}\equiv H,$](img4759.png) |
(G.68) |
so, from Equations (G.62) and (G.65),
![$\displaystyle [p,q] = [p,q]''' + \frac{\partial(\varpi-{\mit\Omega},H )}{\partial (p,q)}
+ \frac{\partial({\mit\Omega}, {\cal G})}{\partial (p,q)}.$](img4760.png) |
(G.69) |
It thus remains to calculate
![$[p,q]'''$](img4761.png) .
.
The coordinates
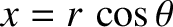 and
and
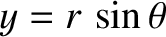 —where
—where  represents radial distance from the Sun, and
represents radial distance from the Sun, and
 is the true anomaly—are functions of the major radius,
is the true anomaly—are functions of the major radius,  ,
the eccentricity,
,
the eccentricity,  , and the mean anomaly,
, and the mean anomaly,
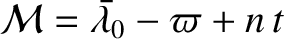 .
Because the Lagrange brackets
are independent of time, it is sufficient to evaluate them at
.
Because the Lagrange brackets
are independent of time, it is sufficient to evaluate them at
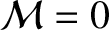 ; that is, at the perihelion point. It is easily
demonstrated from Equations (4.86) and (4.87) that
; that is, at the perihelion point. It is easily
demonstrated from Equations (4.86) and (4.87) that
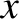 |
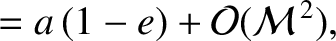 |
(G.70) |
 |
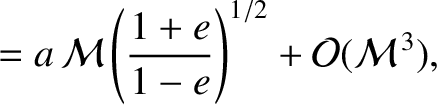 |
(G.71) |
 |
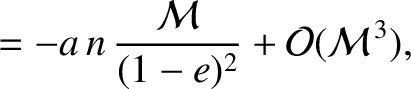 |
(G.72) |
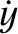 |
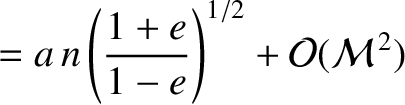 |
(G.73) |
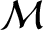 . Hence, at
. Hence, at
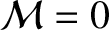 ,
,
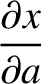 |
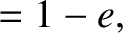 |
(G.74) |
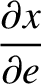 |
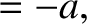 |
(G.75) |
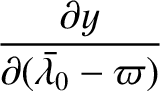 |
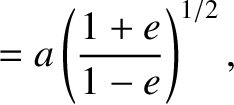 |
(G.76) |
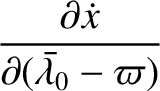 |
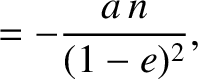 |
(G.77) |
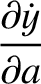 |
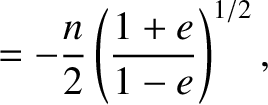 |
(G.78) |
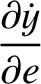 |
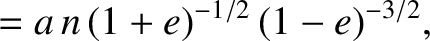 |
(G.79) |
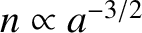 . All other partial derivatives are zero.
Because the orbit in the
. All other partial derivatives are zero.
Because the orbit in the  ,
,  ,
,  coordinate system only
depends on the elements
coordinate system only
depends on the elements  ,
,  , and
, and
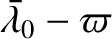 , we
can write
Substitution of the values of the derivatives evaluated at
, we
can write
Substitution of the values of the derivatives evaluated at
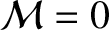 into this expression yields
and
into this expression yields
and
![$\displaystyle [p,q]'''= \frac{\partial(\skew{5}\bar{\lambda}_0-\varpi,a)}{\part...
...2\,a^{1/2}} = \frac{\partial(\skew{5}\bar{\lambda}_0-\varpi,L)}{\partial(p,q)},$](img4791.png) |
(G.84) |
where
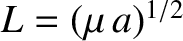 .
Hence, from Equation (G.69), we obtain
.
Hence, from Equation (G.69), we obtain
![$\displaystyle [p,q] = \frac{\partial(\skew{5}\bar{\lambda}_0-\varpi,L)}{\partia...
...H )}{\partial (p,q)}
+ \frac{\partial({\mit\Omega}, {\cal G})}{\partial (p,q)}.$](img4793.png) |
(G.85) |
 ; the mean longitude at epoch,
; the mean longitude at epoch,
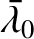 ; the eccentricity,
; the eccentricity,  ;
the inclination (relative to some reference plane),
;
the inclination (relative to some reference plane), 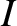 ; the longitude of the perihelion,
; the longitude of the perihelion,
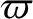 ; and the longitude of the ascending node,
; and the longitude of the ascending node,
 . (See Section 4.12.) The mean orbital angular velocity is
. (See Section 4.12.) The mean orbital angular velocity is
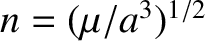 [see Equation (4.117)].
[see Equation (4.117)].
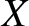 ,
, 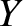 ,
, 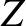 about the
about the 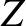 -axis (if we look along the axis).
We can write
-axis (if we look along the axis).
We can write
![$\displaystyle [p,q] = \frac{\partial(X,\dot{X})}{\partial (p,q)}+ \frac{\partial(Y,\dot{Y})}{\partial (p,q)}+ \frac{\partial(Z,\dot{Z})}{\partial (p,q)},$](img4708.png)
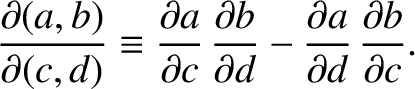
 . A rotation about the
. A rotation about the
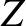 -axis though an angle
-axis though an angle
 brings the ascending node to the
brings the ascending node to the 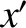 -axis. See Figure 4.6.
The relation between the old and new coordinates is (see Section A.6)
-axis. See Figure 4.6.
The relation between the old and new coordinates is (see Section A.6)
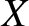
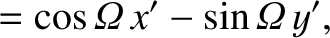
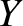
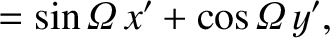
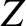
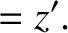
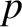 can be written
can be written
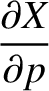
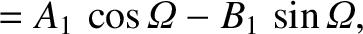
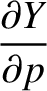
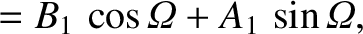
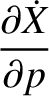
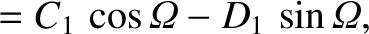
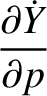
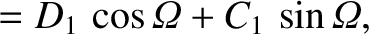
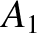
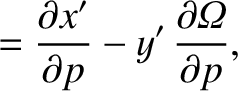
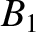
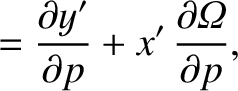
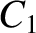
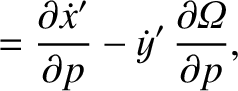
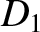
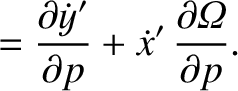
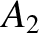 ,
, 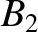 ,
,  , and
, and 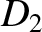 be the equivalent quantities
obtained by replacing
be the equivalent quantities
obtained by replacing 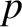 by
by 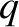 in the preceding equations.
It thus follows that
in the preceding equations.
It thus follows that
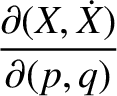
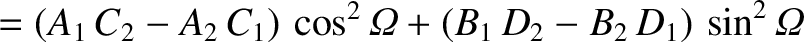
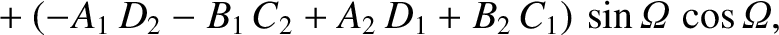
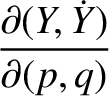
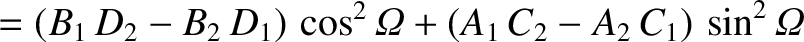
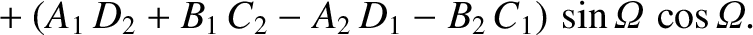
![$\displaystyle [p,q] = A_1\,C_2-A_2\,C_1 + B_1\,D_2-B_2\,D_1+ \frac{\partial(Z,\dot{Z})}{\partial(p,q)}.$](img4735.png)
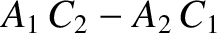
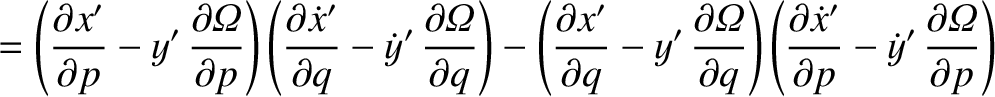
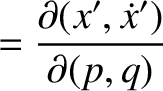
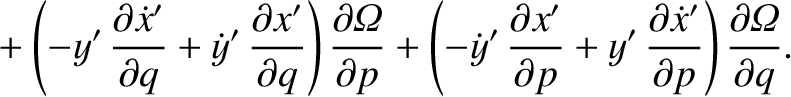
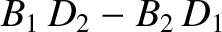
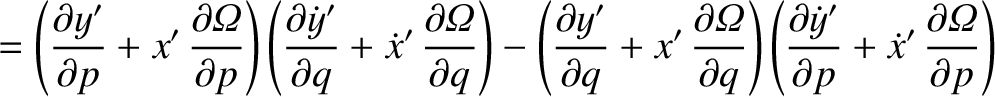
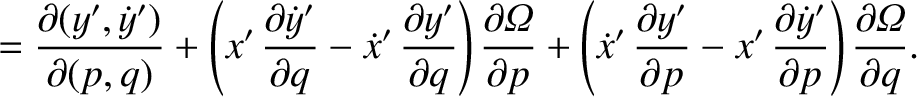
![$\displaystyle [p,q]' = \frac{\partial(x',\dot{x}')}{\partial (p,q)}+ \frac{\partial(y',\dot{y}')}{\partial (p,q)}+ \frac{\partial(z',\dot{z}')}{\partial (p,q)}.$](img4743.png)
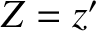 and
and
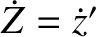 , it follows that
, it follows that
![$\displaystyle [p,q]$](img4746.png)
![$\displaystyle = [p,q]' + \left(x'\,\frac{\partial \dot{y}'}{\partial q}+ \dot{y...
...'\,\frac{\partial y'}{\partial q}\right)\frac{\partial{\mit\Omega}}{\partial p}$](img4747.png)
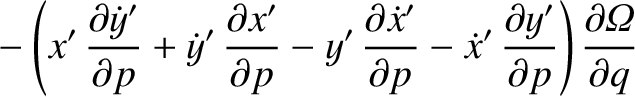
![$\displaystyle = [p,q]' + \frac{\partial({\mit\Omega}, x'\,\dot{y}'-y'\,\dot{x}')}{\partial (p,q)}.$](img4749.png)
![$\displaystyle x'\,\dot{y}'-y'\,\dot{x}' = h\,\cos\,I = [\mu\,a\,(1-e^{\,2})]^{1/2}\,\cos\,I \equiv {\cal G},$](img4750.png)
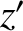 -axis. Of course, this axis is inclined at an angle
-axis. Of course, this axis is inclined at an angle 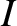 to the
to the  -axis, which is parallel to the angular momentum vector.
Thus, we obtain
-axis, which is parallel to the angular momentum vector.
Thus, we obtain
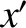 -axis. Let the
new coordinate system be
-axis. Let the
new coordinate system be 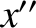 ,
, 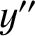 ,
, 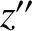 . A rotation through an
angle
. A rotation through an
angle 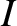 brings the orbit into the
brings the orbit into the 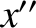 -
-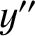 plane. See Figure 4.6.
Let
plane. See Figure 4.6.
Let
![$\displaystyle [p,q]'' = \frac{\partial(x'',\dot{x}'')}{\partial (p,q)}+ \frac{\...
...'',\dot{y}'')}{\partial (p,q)}+ \frac{\partial(z'',\dot{z}'')}{\partial (p,q)}.$](img4752.png)
![$\displaystyle [p,q]' = [p,q]'' + \frac{\partial(I,y''\,\dot{z}''-z''\,\dot{y}'')}{\partial(p,q)}.$](img4753.png)
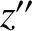 and
and 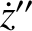 are both zero, because the orbit lies
in the
are both zero, because the orbit lies
in the 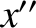 -
-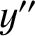 plane. Hence,
plane. Hence,
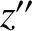 -axis. Let the
final coordinate system be
-axis. Let the
final coordinate system be  ,
,  ,
,  . A rotation through an angle
. A rotation through an angle
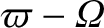 brings the perihelion to the
brings the perihelion to the  -axis. See Figure 4.6.
Let
-axis. See Figure 4.6.
Let
![$\displaystyle [p,q]''' = \frac{\partial(x,\dot{x})}{\partial (p,q)}+ \frac{\partial(y,\dot{y})}{\partial (p,q)}.$](img4757.png)
![$\displaystyle [p,q]'' = [p,q]''' + \frac{\partial(\varpi-{\mit\Omega},x\,\dot{y}-y\,\dot{x})}{\partial (p,q)}.$](img4758.png)
![$\displaystyle x\,\dot{y}-y\,\dot{x} = h= [\mu\,a\,(1-e^{\,2})]^{1/2}\equiv H,$](img4759.png)
![$[p,q]'''$](img4761.png) .
.
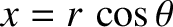 and
and
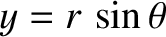 —where
—where  represents radial distance from the Sun, and
represents radial distance from the Sun, and
 is the true anomaly—are functions of the major radius,
is the true anomaly—are functions of the major radius,  ,
the eccentricity,
,
the eccentricity,  , and the mean anomaly,
, and the mean anomaly,
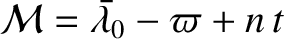 .
Because the Lagrange brackets
are independent of time, it is sufficient to evaluate them at
.
Because the Lagrange brackets
are independent of time, it is sufficient to evaluate them at
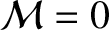 ; that is, at the perihelion point. It is easily
demonstrated from Equations (4.86) and (4.87) that
; that is, at the perihelion point. It is easily
demonstrated from Equations (4.86) and (4.87) that
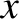
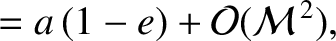
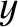
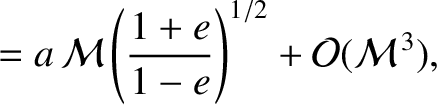
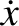
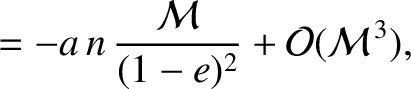
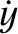
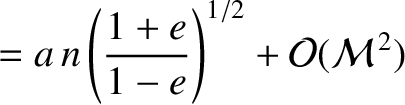
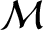 . Hence, at
. Hence, at
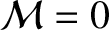 ,
,
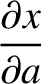
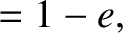
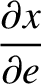
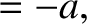
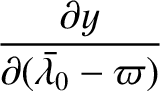
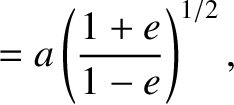
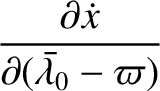
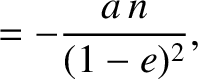
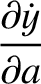
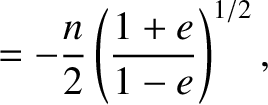
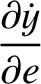
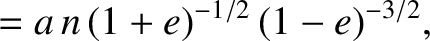
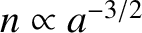 . All other partial derivatives are zero.
Because the orbit in the
. All other partial derivatives are zero.
Because the orbit in the  ,
,  ,
,  coordinate system only
depends on the elements
coordinate system only
depends on the elements  ,
,  , and
, and
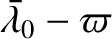 , we
can write
, we
can write
![$\displaystyle [p,q]'''$](img4783.png)
![$\displaystyle =\frac{\partial(a,e)}{\partial(p,q)}\left[\frac{\partial(x,\dot{x})}{\partial(a,e)}+\frac{\partial(y,\dot{y})}{\partial(a,e)}\right]$](img4784.png)
![$\displaystyle \phantom{=}+\frac{\partial(e,\skew{5}\bar{\lambda}_0-\varpi)}{\pa...
...}+\frac{\partial(y,\dot{y})}{\partial(e,\skew{5}\bar{\lambda}_0-\varpi)}\right]$](img4785.png)
![$\displaystyle \phantom{=}+\frac{\partial(\skew{5}\bar{\lambda}_0-\varpi,a)}{\pa...
...+\frac{\partial(y,\dot{y})}{\partial(\skew{5}\bar{\lambda}_0-\varpi,a)}\right].$](img4786.png)
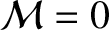 into this expression yields
into this expression yields
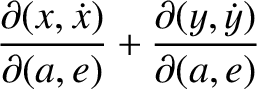
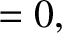
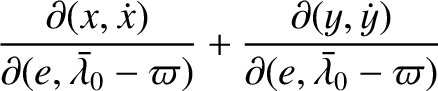
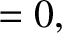
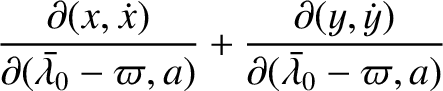
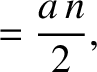
![$\displaystyle [p,q]'''= \frac{\partial(\skew{5}\bar{\lambda}_0-\varpi,a)}{\part...
...2\,a^{1/2}} = \frac{\partial(\skew{5}\bar{\lambda}_0-\varpi,L)}{\partial(p,q)},$](img4791.png)
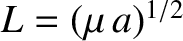 .
Hence, from Equation (G.69), we obtain
.
Hence, from Equation (G.69), we obtain