Next: Elliptic expansions Up: Useful mathematics Previous: Curvilinear coordinates
An ellipse, centered on the origin, of major radius  and minor radius
and minor radius 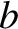 , that are aligned
along the
, that are aligned
along the  - and
- and  -axes, respectively (see Figure A.4), satisfies the following
well-known equation:
-axes, respectively (see Figure A.4), satisfies the following
well-known equation:
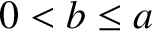 .
.
Likewise, a parabola that is aligned along the 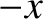 -axis, and passes through
the origin (see Figure A.5), satisfies
-axis, and passes through
the origin (see Figure A.5), satisfies
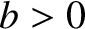 .
.
Finally, a hyperbola that is aligned along the 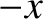 -axis, and whose
asymptotes intersect at the origin (see Figure A.6), satisfies
-axis, and whose
asymptotes intersect at the origin (see Figure A.6), satisfies
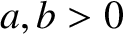 .
Here,
.
Here,  is the distance of closest approach to the origin. The
asymptotes subtend an angle
is the distance of closest approach to the origin. The
asymptotes subtend an angle
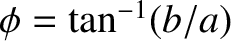 with the
with the 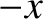 -axis.
-axis.
It is not obvious, from the preceding formulae, what the ellipse, the parabola, and the hyperbola
have in common. It turns out, in fact, that these three curves
can all be represented as the locus of a movable point whose distance from
a fixed point is in a constant ratio to its perpendicular distance to some
fixed straight line. Let the fixed point—which is termed the focus—lie at the origin, and let
the fixed line—which is termed the directrix—correspond to 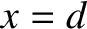 (with
(with  ). Thus, the distance of a general point (
). Thus, the distance of a general point ( ,
,  ) (which lies to the left of the directrix) from the focus is
) (which lies to the left of the directrix) from the focus is
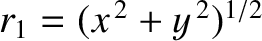 , whereas the perpendicular distance of the point from
the directrix is
, whereas the perpendicular distance of the point from
the directrix is 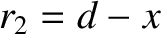 . See Figure A.7.
In polar coordinates,
. See Figure A.7.
In polar coordinates, 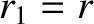 and
and
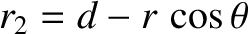 .
Hence, the locus of a point for which
.
Hence, the locus of a point for which
 and
and 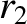 are in a fixed ratio satisfies the following equation:
are in a fixed ratio satisfies the following equation:
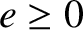 is a constant. When expressed in terms of
polar coordinates, the preceding equation can be rearranged to give
where
is a constant. When expressed in terms of
polar coordinates, the preceding equation can be rearranged to give
where 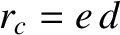 .
.
When written in terms of Cartesian coordinates, Equation (A.104) can be rearranged to give
for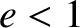 . Here,
Equation (A.106) can be recognized as the equation of an ellipse
whose center lies at (
. Here,
Equation (A.106) can be recognized as the equation of an ellipse
whose center lies at (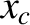 , 0), and whose major and minor radii,
, 0), and whose major and minor radii,
 and
and 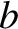 , are aligned along the
, are aligned along the  - and
- and  -axes, respectively
[see Equation (A.101)]. Note, incidentally, that an ellipse
actually possesses two focii located on the major axis (
-axes, respectively
[see Equation (A.101)]. Note, incidentally, that an ellipse
actually possesses two focii located on the major axis (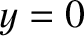 ) a distance
) a distance 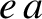 on either side of the
geometric center (i.e., at
on either side of the
geometric center (i.e., at 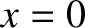 and
and
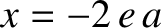 ). Likewise, an ellipse possesses two directrices located
at
). Likewise, an ellipse possesses two directrices located
at
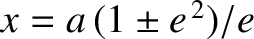 .
.
When again written in terms of Cartesian coordinates, Equation (A.104) can be rearranged to give
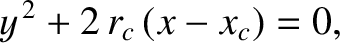 |
(A.110) |
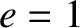 . Here,
. Here,
 . This is the equation of a parabola
that passes through the point (
. This is the equation of a parabola
that passes through the point (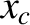 , 0), and that is aligned
along the
, 0), and that is aligned
along the 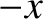 -direction [see Equation (A.102)].
-direction [see Equation (A.102)].
Finally, when written in terms of Cartesian coordinates, Equation (A.104) can be rearranged to give
for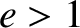 . Here,
. Here,
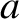 |
 |
(A.112) |
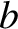 |
 |
(A.113) |
 |
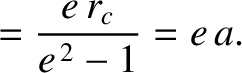 |
(A.114) |
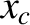 , 0), and that
is aligned along the
, 0), and that
is aligned along the 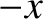 -direction. The asymptotes subtend an angle
-direction. The asymptotes subtend an angle
 |
(A.115) |
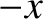 -axis [see Equation (A.103)].
-axis [see Equation (A.103)].
In conclusion, Equation (A.105) is the polar equation of a general conic
section that is confocal with the origin (i.e., the origin lies at a focus). For 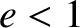 , the conic section
is an ellipse. For
, the conic section
is an ellipse. For 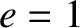 , the conic section is a parabola. Finally, for
, the conic section is a parabola. Finally, for
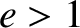 , the conic section is a hyperbola.
, the conic section is a hyperbola.