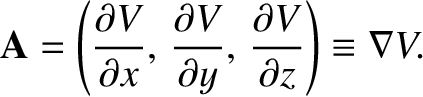Conservative fields
Consider a vector field
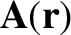 . In general, the line integral
. In general, the line integral
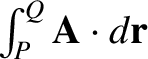 depends on the path
taken between the end points,
depends on the path
taken between the end points, 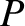 and
and 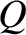 .
However, for some special vector fields the integral is path independent. Such fields
are called conservative fields. It can be shown that if
.
However, for some special vector fields the integral is path independent. Such fields
are called conservative fields. It can be shown that if 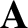 is a
conservative field then
is a
conservative field then
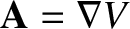 for some scalar field
for some scalar field
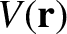 .
The proof of this is straightforward. Keeping
.
The proof of this is straightforward. Keeping 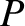 fixed, we have
fixed, we have
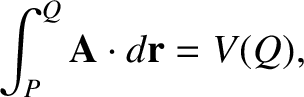 |
(A.82) |
where 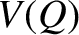 is a well-defined function, due to the path-independent nature of the
line integral. Consider moving the position of the end point by an infinitesimal
amount
is a well-defined function, due to the path-independent nature of the
line integral. Consider moving the position of the end point by an infinitesimal
amount 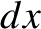 in the
in the  -direction. We have
-direction. We have
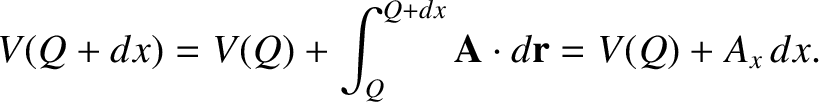 |
(A.83) |
Hence,
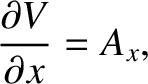 |
(A.84) |
with analogous relations for the other components of 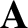 . It follows that
. It follows that
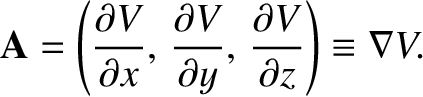 |
(A.85) |
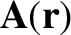 . In general, the line integral
. In general, the line integral
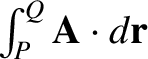 depends on the path
taken between the end points,
depends on the path
taken between the end points,  and
and  .
However, for some special vector fields the integral is path independent. Such fields
are called conservative fields. It can be shown that if
.
However, for some special vector fields the integral is path independent. Such fields
are called conservative fields. It can be shown that if 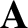 is a
conservative field then
is a
conservative field then
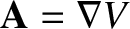 for some scalar field
for some scalar field
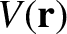 .
The proof of this is straightforward. Keeping
.
The proof of this is straightforward. Keeping 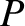 fixed, we have
fixed, we have
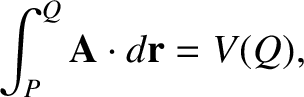
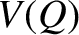 is a well-defined function, due to the path-independent nature of the
line integral. Consider moving the position of the end point by an infinitesimal
amount
is a well-defined function, due to the path-independent nature of the
line integral. Consider moving the position of the end point by an infinitesimal
amount 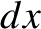 in the
in the  -direction. We have
-direction. We have
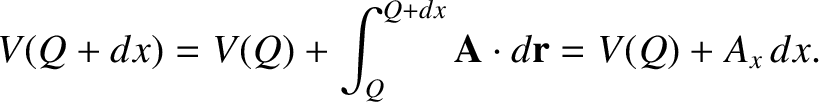
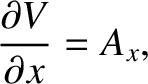
 . It follows that
. It follows that