Next: Co-rotating frame Up: Three-body problem Previous: Jacobi integral
 ,
, 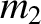 , and
, and  . Let mass
. Let mass  represent the Sun, mass
represent the Sun, mass 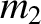 the planet Jupiter, and mass
the planet Jupiter, and mass  a comet. Because the
mass of a comet is very much less than that of the Sun or Jupiter, and the Sun and Jupiter
are in (almost) circular orbits about their common center of mass, the dynamical system in question satisfies
all of the necessary criteria to be considered an example of a restricted three-body problem.
a comet. Because the
mass of a comet is very much less than that of the Sun or Jupiter, and the Sun and Jupiter
are in (almost) circular orbits about their common center of mass, the dynamical system in question satisfies
all of the necessary criteria to be considered an example of a restricted three-body problem.
The mass of the Sun is much greater than that of Jupiter. It follows that the gravitational effect of Jupiter on the cometary orbit is negligible unless the comet makes a very close approach to Jupiter. Hence, as described in Chapter 4, before and after such an approach, the comet executes a Keplerian elliptical orbit about the Sun with fixed orbital parameters; that is, fixed major radius, eccentricity, and inclination to the ecliptic plane. However, in general, the orbital parameters before and after the close approach will not be the same as one another. Let us investigate further.
Because
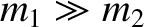 , we have
, we have
 , and
, and
 .
Hence, according to Equations (4.34) and (4.44), the (approximately) conserved
energy (per unit mass) of the comet before and after its close approach to Jupiter is
.
Hence, according to Equations (4.34) and (4.44), the (approximately) conserved
energy (per unit mass) of the comet before and after its close approach to Jupiter is
 . (Incidentally, we are working
in units such that the major radius of Jupiter's orbit is unity.) Furthermore, the (approximately) conserved
angular momentum (per unit mass) of the comet before and after its approach to Jupiter
is written
. (Incidentally, we are working
in units such that the major radius of Jupiter's orbit is unity.) Furthermore, the (approximately) conserved
angular momentum (per unit mass) of the comet before and after its approach to Jupiter
is written 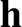 , where
, where 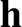 is directed normal to the comet's orbital plane,
and, from Equations (4.31) and (A.107),
is directed normal to the comet's orbital plane,
and, from Equations (4.31) and (A.107),
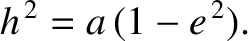 |
(9.17) |
 is the comet's orbital eccentricity. It follows that
because
is the comet's orbital eccentricity. It follows that
because  in our adopted system of units. Here,
in our adopted system of units. Here,  is the angle of
inclination of the normal to the comet's orbital plane to that of Jupiter's orbital
plane.
is the angle of
inclination of the normal to the comet's orbital plane to that of Jupiter's orbital
plane.
![\includegraphics[height=3.5in]{Chapter08/fig8_02.eps}](img2132.png)
|
Let  ,
,  , and
, and  be the major radius, eccentricity, and inclination angle of the cometary
orbit before the close encounter with Jupiter, and let
be the major radius, eccentricity, and inclination angle of the cometary
orbit before the close encounter with Jupiter, and let 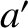 ,
, 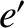 , and
, and  be the corresponding
parameters after the encounter. It follows from Equations (9.15), (9.16), and
(9.18), and the fact that
be the corresponding
parameters after the encounter. It follows from Equations (9.15), (9.16), and
(9.18), and the fact that  is conserved during the encounter, whereas
is conserved during the encounter, whereas
 and
and 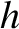 are not, that
are not, that
![\includegraphics[height=3.5in]{Chapter08/fig8_03.eps}](img2136.png)
|
The Tisserand criterion is extremely useful. For instance, whenever a new comet is discovered, astronomers immediately calculate its Tisserand parameter,
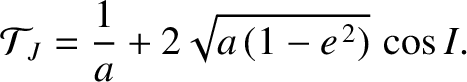 |
(9.20) |
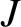 in the preceding formula is to remind us that we are dealing with the
Tisserand parameter for close encounters with Jupiter. (The parameter is, thus, evaluated
in a system of units in which the major radius of Jupiter's orbit is unity). Obviously,
it is also possible to calculate Tisserand parameters for close encounters with other massive planets.
in the preceding formula is to remind us that we are dealing with the
Tisserand parameter for close encounters with Jupiter. (The parameter is, thus, evaluated
in a system of units in which the major radius of Jupiter's orbit is unity). Obviously,
it is also possible to calculate Tisserand parameters for close encounters with other massive planets.
![\includegraphics[height=3.75in]{Chapter08/fig8_04.eps}](img2139.png)
|
Figure 9.2 shows the changing orbit of a hypothetical comet that has a close approach to Jupiter. The initial
orbit is such that  (in units in which the major radius of the Jovian orbit is unity),
(in units in which the major radius of the Jovian orbit is unity), 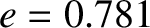 , and
, and 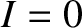 , whereas
the final orbit is such that
, whereas
the final orbit is such that  ,
, 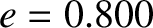 , and
, and 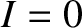 . Figure 9.3 shows the comet's major radius,
. Figure 9.3 shows the comet's major radius,  ,
eccentricity,
,
eccentricity,  , and Tisserand parameter,
, and Tisserand parameter,
 , as functions of time, before, during, and after, the
encounter with Jupiter. It can be seen that the major radius and the eccentricity are both modified by the
encounter (which occurs when
, as functions of time, before, during, and after, the
encounter with Jupiter. It can be seen that the major radius and the eccentricity are both modified by the
encounter (which occurs when
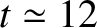 ), while the Tisserand parameter remains
constant in time. This remains true even when the small eccentricity of the Jovian orbit is taken into account in the calculation.
), while the Tisserand parameter remains
constant in time. This remains true even when the small eccentricity of the Jovian orbit is taken into account in the calculation.
The Tisserand parameter is often employed to distinguish between comets and asteroids in the solar system. This idea is illustrated in
Figure 9.4, which shows the Jovian Tisserand parameter,
 , plotted against the major radius,
, plotted against the major radius,  ,
of the principal asteroids and comets in the solar system. The Tisserand parameter of Jupiter (which is almost exactly three) is
also shown. It can be seen that, roughly speaking, asteroids have higher Tisserand parameters than Jupiter, whereas
comets have lower Tisserand parameters. The only major exception to this rule is the so-called Trojan asteroids (see Section 9.8), which all have very similar major radii to Jupiter (because, by definition, they must have the same
orbital period as Jupiter), and consequently have lower Tisserand parameters (because they generally have higher eccentricities and inclinations than Jupiter).
The lower Tisserand parameters of comets with respect to Jupiter, and of Jupiter with respect to regular asteroids, is indicative of the fact that comets generally originated beyond the Jovian orbit, whereas regular asteroids generally originated within the Jovian orbit.
,
of the principal asteroids and comets in the solar system. The Tisserand parameter of Jupiter (which is almost exactly three) is
also shown. It can be seen that, roughly speaking, asteroids have higher Tisserand parameters than Jupiter, whereas
comets have lower Tisserand parameters. The only major exception to this rule is the so-called Trojan asteroids (see Section 9.8), which all have very similar major radii to Jupiter (because, by definition, they must have the same
orbital period as Jupiter), and consequently have lower Tisserand parameters (because they generally have higher eccentricities and inclinations than Jupiter).
The lower Tisserand parameters of comets with respect to Jupiter, and of Jupiter with respect to regular asteroids, is indicative of the fact that comets generally originated beyond the Jovian orbit, whereas regular asteroids generally originated within the Jovian orbit.
The Tisserand criterion is also applicable to so-called gravity assists, in which a
spacecraft gains energy due to a close encounter with a moving planet. Such assists
are often employed in missions to the outer planets to reduce the amount of fuel
which the spacecraft must carry in order to reach its destination. In fact, it is clear,
from Equations (9.16) and (9.19), that a spacecraft can make use of a close encounter
with a moving planet to increase (or decrease) its orbital major radius  , and, hence, to increase
(or decrease)
its total orbital energy.
, and, hence, to increase
(or decrease)
its total orbital energy.