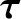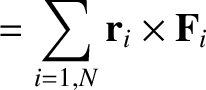Non-isolated systems
Up to now, we have only considered isolated dynamical systems, in which all of the forces acting
on the system originate from within the system itself. Let us now generalize our approach to
deal with non-isolated dynamical systems, in which some of the forces originate outside the system. Consider a system of 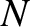 mutually interacting point objects. Let
mutually interacting point objects. Let
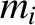 and
and 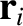 be the mass and position vector of the
be the mass and position vector of the  th object, respectively. Suppose
that the
th object, respectively. Suppose
that the  th object is subject to two forces: first, an internal force that originates
from the other objects in the system; and, second, an external force that originates
outside the system. In other words, let the force acting on the
th object is subject to two forces: first, an internal force that originates
from the other objects in the system; and, second, an external force that originates
outside the system. In other words, let the force acting on the  th object take the form
th object take the form
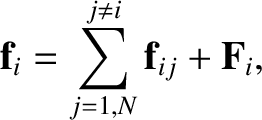 |
(2.38) |
where
 is the internal force exerted by object
is the internal force exerted by object 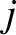 on object
on object  , and
, and 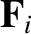 the
external force acting on object
the
external force acting on object  .
.
The equation of motion of the  th object is
th object is
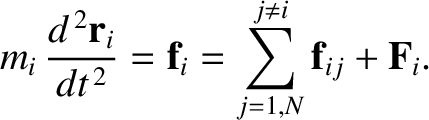 |
(2.39) |
Summing over all objects, we obtain
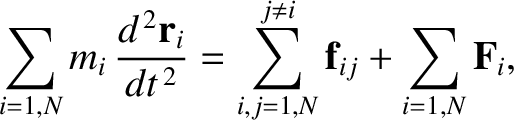 |
(2.40) |
which reduces to
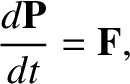 |
(2.41) |
where
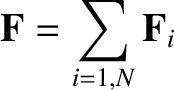 |
(2.42) |
is the net external force acting on the system. Here, the sum over the internal forces has cancelled out in pairs
as a result of Newton's third law of motion. (See Section 2.5.) We conclude that if there is a net external force acting on the system then the total linear momentum evolves in time according to
Equation (2.41) but is completely unaffected by any internal forces.
The fact that Equation (2.41) is similar in form to Equation (2.13) suggests that the center of
mass of a system consisting of many point objects has analogous dynamics to a single point object, whose mass
is the total system mass, moving under the
action of the net external force.
Taking
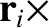 Equation (2.39), and summing over all objects, we obtain
Equation (2.39), and summing over all objects, we obtain
where
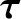 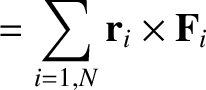 |
(2.44) |
is the net external torque (about the origin) acting on the system. Here, the sum over the internal
torques has cancelled out in pairs, assuming that the internal forces are central in nature. (See Section 2.5.)
We conclude that if there is a net external torque acting on the system then the total angular momentum evolves in time according to the simple equation (2.43) but is completely unaffected by any internal torques.
 mutually interacting point objects. Let
mutually interacting point objects. Let
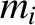 and
and 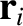 be the mass and position vector of the
be the mass and position vector of the  th object, respectively. Suppose
that the
th object, respectively. Suppose
that the  th object is subject to two forces: first, an internal force that originates
from the other objects in the system; and, second, an external force that originates
outside the system. In other words, let the force acting on the
th object is subject to two forces: first, an internal force that originates
from the other objects in the system; and, second, an external force that originates
outside the system. In other words, let the force acting on the  th object take the form
th object take the form
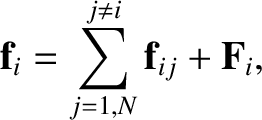
 is the internal force exerted by object
is the internal force exerted by object 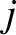 on object
on object  , and
, and 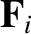 the
external force acting on object
the
external force acting on object  .
.
 th object is
th object is
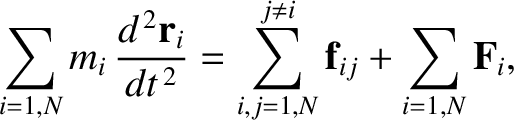
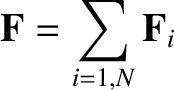
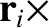 Equation (2.39), and summing over all objects, we obtain
Equation (2.39), and summing over all objects, we obtain