Next: Rotational kinetic energy Up: Rigid body rotation Previous: Fundamental equations
 about
an axis that passes through the origin. See Figure 8.1.
Let
about
an axis that passes through the origin. See Figure 8.1.
Let 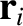 be the position vector of the
be the position vector of the  th mass element, whose mass
is
th mass element, whose mass
is 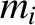 .
We expect this position vector to precess about the axis of rotation
(which is parallel to
.
We expect this position vector to precess about the axis of rotation
(which is parallel to
 )
with angular velocity
)
with angular velocity  . It, therefore, follows from Section A.7
that
Thus, Equation (8.4) specifies the velocity,
. It, therefore, follows from Section A.7
that
Thus, Equation (8.4) specifies the velocity,
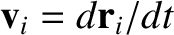 ,
of each mass element as the body rotates with fixed angular velocity
,
of each mass element as the body rotates with fixed angular velocity
 about
an axis passing through the origin.
about
an axis passing through the origin.
The total angular momentum of the body (about the origin) is written
where use has been made of Equation (8.4), and some standard vector identities. (See Section A.4.) The preceding formula can be written as a matrix equation of the form where Here,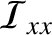 is called the moment of inertia about the
is called the moment of inertia about the  -axis,
-axis,
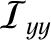 the moment of inertia about the
the moment of inertia about the  -axis,
-axis,
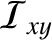 the
the  product of inertia,
product of inertia,
 the
the  product of
inertia, and so on. The matrix of the
product of
inertia, and so on. The matrix of the
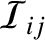 values is
known as the moment of inertia tensor. Each component
of the moment of inertia tensor can be written as either a sum over separate
mass elements, or as an integral over infinitesimal mass elements.
In the integrals,
values is
known as the moment of inertia tensor. Each component
of the moment of inertia tensor can be written as either a sum over separate
mass elements, or as an integral over infinitesimal mass elements.
In the integrals,
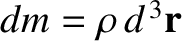 , where
, where 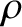 is the mass density, and
is the mass density, and
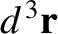 a volume element.
Equation (8.6) can be written more succinctly as
Here, it is understood that
a volume element.
Equation (8.6) can be written more succinctly as
Here, it is understood that 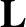 and
and
 are
both column vectors, and
are
both column vectors, and
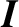 is the matrix of the
is the matrix of the
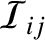 values.
Note that
values.
Note that
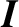 is a real symmetric matrix; that is,
is a real symmetric matrix; that is,
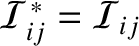 and
and
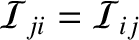 .
.
In general,
the angular momentum vector, 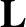 , obtained from Equation (8.13),
points in a different direction to the angular velocity vector,
, obtained from Equation (8.13),
points in a different direction to the angular velocity vector,
 . In other words,
. In other words, 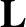 is generally not parallel to
is generally not parallel to
 .
.
Finally, although the preceding results were obtained assuming a fixed angular velocity they remain valid, at each instant in time, if the angular velocity varies.