Next: Centrifugal acceleration Up: Rotating reference frames Previous: Introduction
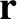 in some inertial (i.e., non-rotating) reference frame. Let us observe the motion of
this object in a non-inertial reference frame that rotates with constant angular
velocity
in some inertial (i.e., non-rotating) reference frame. Let us observe the motion of
this object in a non-inertial reference frame that rotates with constant angular
velocity
 about
an axis passing through the origin of the inertial frame. Suppose, first of all, that our object appears stationary in the rotating reference frame. Hence, in the non-rotating frame,
the object's position vector
about
an axis passing through the origin of the inertial frame. Suppose, first of all, that our object appears stationary in the rotating reference frame. Hence, in the non-rotating frame,
the object's position vector 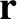 will appear to precess about the origin with
angular velocity
will appear to precess about the origin with
angular velocity
 . It follows from Section A.7
that, in the non-rotating reference frame,
. It follows from Section A.7
that, in the non-rotating reference frame,
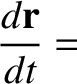  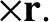 |
(6.1) |
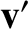 . It is fairly obvious that the appropriate generalization of the preceding equation is simply
. It is fairly obvious that the appropriate generalization of the preceding equation is simply
Let 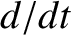 and
and 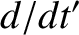 denote apparent time derivatives in the non-rotating and rotating frames of reference, respectively. Because an object that is
stationary in the rotating reference frame appears to move in the non-rotating
frame, it is clear that
denote apparent time derivatives in the non-rotating and rotating frames of reference, respectively. Because an object that is
stationary in the rotating reference frame appears to move in the non-rotating
frame, it is clear that
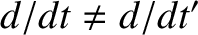 . Writing the apparent velocity,
. Writing the apparent velocity, 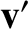 ,
of our object in the rotating reference frame as
,
of our object in the rotating reference frame as
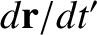 , Equation (6.2) takes the form
, Equation (6.2) takes the form
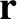 is a general position vector. Equation (6.4) expresses the
relationship between apparent time derivatives in the non-rotating and
rotating reference frames.
is a general position vector. Equation (6.4) expresses the
relationship between apparent time derivatives in the non-rotating and
rotating reference frames.
Operating on the general position vector 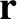 with the time derivative in Equation (6.4), we get
with the time derivative in Equation (6.4), we get
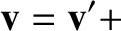  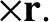 |
(6.5) |
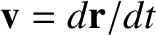 , of an object with
position vector
, of an object with
position vector 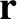 in the non-rotating reference frame to its
apparent velocity,
in the non-rotating reference frame to its
apparent velocity,
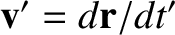 , in the rotating reference frame.
, in the rotating reference frame.
Operating twice on the position vector 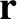 with the time
derivative in Equation (6.4), we obtain
with the time
derivative in Equation (6.4), we obtain
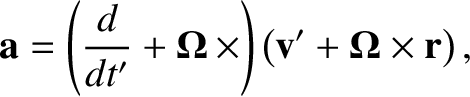 |
(6.6) |
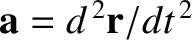 , of an object with
position vector
, of an object with
position vector 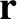 in the non-rotating reference frame to its
apparent acceleration,
in the non-rotating reference frame to its
apparent acceleration,
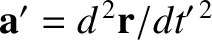 , in the rotating reference frame.
, in the rotating reference frame.
Applying Newton's second law of motion in the inertial (i.e., non-rotating) reference frame, we obtain
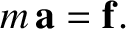 |
(6.8) |
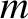 is the mass of our object, and
is the mass of our object, and 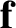 is the (non-fictitious) force acting on it. These quantities are the same in both reference
frames.
Making use of Equation (6.7), the apparent equation of motion of our object in the
rotating reference frame takes the form
The last two terms in this equation are so-called fictitious forces; such forces
are always needed to account for motion observed in non-inertial reference
frames. Fictitious forces can always be distinguished from
non-fictitious forces in Newtonian mechanics because the former
have no associated reactions.
Let us now investigate the two fictitious forces appearing in Equation (6.9).
is the (non-fictitious) force acting on it. These quantities are the same in both reference
frames.
Making use of Equation (6.7), the apparent equation of motion of our object in the
rotating reference frame takes the form
The last two terms in this equation are so-called fictitious forces; such forces
are always needed to account for motion observed in non-inertial reference
frames. Fictitious forces can always be distinguished from
non-fictitious forces in Newtonian mechanics because the former
have no associated reactions.
Let us now investigate the two fictitious forces appearing in Equation (6.9).