Next: Rotating reference frames Up: Orbits in central force Previous: Perihelion precession of Mercury
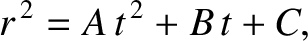
 ,
, 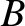 ,
,  are constants. (From Lamb 1923.)
are constants. (From Lamb 1923.)
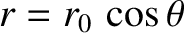 , where
, where  . Show that the force law
is inverse fifth power. (Modified from Fowles and Cassiday 2005.)
. Show that the force law
is inverse fifth power. (Modified from Fowles and Cassiday 2005.)
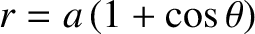 , where
, where  . Show that the force law
is inverse fourth power.
. Show that the force law
is inverse fourth power.
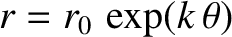 , where
, where 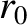 ,
, 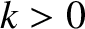 .
Show that the force law is inverse cube, and that
.
Show that the force law is inverse cube, and that  varies logarithmically with
varies logarithmically with 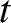 .
Demonstrate that there are two other possible types of orbit in this force field, and give their
equations. (Modified from Fowles and Cassiday 2005.)
.
Demonstrate that there are two other possible types of orbit in this force field, and give their
equations. (Modified from Fowles and Cassiday 2005.)
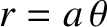 , where
, where  . Suppose that
. Suppose that  increases linearly
with
increases linearly
with 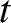 . Is the force acting on the particle central in nature? If not, determine how
. Is the force acting on the particle central in nature? If not, determine how  would have to
vary with
would have to
vary with 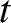 in order to make the force central. Assuming that the force is central,
demonstrate that the particle's potential energy per unit mass is
in order to make the force central. Assuming that the force is central,
demonstrate that the particle's potential energy per unit mass is
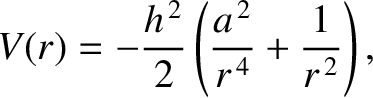
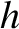 is its (constant) angular momentum per unit mass.
(Modified from Fowles and Cassiday 2005.)
is its (constant) angular momentum per unit mass.
(Modified from Fowles and Cassiday 2005.)
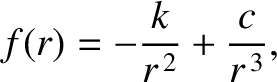
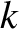 and
and 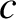 are positive constants. Show that the associated orbit can be written
are positive constants. Show that the associated orbit can be written
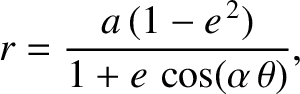
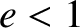 and
and  . Discuss the character of the orbit for
. Discuss the character of the orbit for
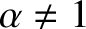 and
and 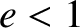 .
Demonstrate that
.
Demonstrate that
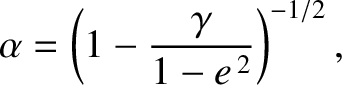
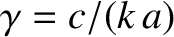 .
.
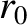 in an attractive
central force field of the form
in an attractive
central force field of the form
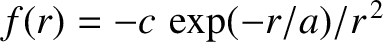 , where
, where  and
and  .
Demonstrate that the orbit is only stable provided that
.
Demonstrate that the orbit is only stable provided that 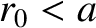 .
.
 , where
, where  . Show
that the orbit is unstable to small perturbations.
. Show
that the orbit is unstable to small perturbations.
 under the action of the radial
force per unit mass
under the action of the radial
force per unit mass
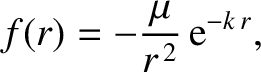
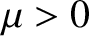 and
and
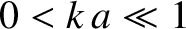 . Demonstrate that the so-called apse line, joining successive apse points, rotates
in the same direction as the orbital motion through an angle
. Demonstrate that the so-called apse line, joining successive apse points, rotates
in the same direction as the orbital motion through an angle 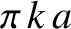 each revolution. (From Lamb 1923.)
each revolution. (From Lamb 1923.)
 under the action of the central potential
per unit mass
under the action of the central potential
per unit mass
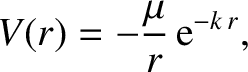
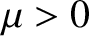 and
and
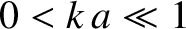 . Show that the apse line rotates
in the same direction as the orbital motion through an angle
. Show that the apse line rotates
in the same direction as the orbital motion through an angle
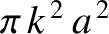 each revolution. (From Lamb 1923.)
each revolution. (From Lamb 1923.)

 is the mass of the Sun, and
is the mass of the Sun, and 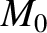 is the mass of dust enclosed by a sphere whose radius matches the
major radius of the orbit. It is assumed that
is the mass of dust enclosed by a sphere whose radius matches the
major radius of the orbit. It is assumed that 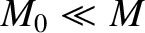 .
.
 and ellipticity
and ellipticity  (where
(where
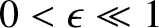 ). Suppose that the orbit
is nearly circular, with a major radius
). Suppose that the orbit
is nearly circular, with a major radius  , and lies in the equatorial plane of the planet. The potential
energy per unit mass of the satellite is thus (see Chapter 3)
, and lies in the equatorial plane of the planet. The potential
energy per unit mass of the satellite is thus (see Chapter 3)
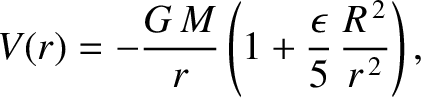
 is a radial coordinate in the equatorial plane. Demonstrate that the apse line rotates in the same
direction as the orbital motion at the rate
is a radial coordinate in the equatorial plane. Demonstrate that the apse line rotates in the same
direction as the orbital motion at the rate
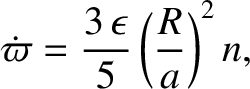
 is the mean orbital angular velocity of the satellite.
is the mean orbital angular velocity of the satellite.