Next: Binary star systems Up: Keplerian orbits Previous: Parabolic orbits
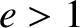 ,
similar analysis to that in Section 4.11 gives,
Here,
,
similar analysis to that in Section 4.11 gives,
Here, 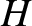 is termed the hyperbolic anomaly, and varies between
is termed the hyperbolic anomaly, and varies between
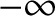 and
and  , with the perihelion point corresponding to
, with the perihelion point corresponding to 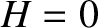 . Moreover,
. Moreover,
 . As in the elliptical
case, Equation (4.105) is a transcendental equation that is most easily solved numerically.
. As in the elliptical
case, Equation (4.105) is a transcendental equation that is most easily solved numerically.