Next: Hyperbolic orbits Up: Keplerian orbits Previous: Planetary orbits
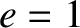 , similar analysis to
that in Section 4.11 yields,
Here,
, similar analysis to
that in Section 4.11 yields,
Here, 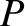 is termed the parabolic anomaly and varies between
is termed the parabolic anomaly and varies between
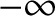 and
and  , with the perihelion point corresponding to
, with the perihelion point corresponding to  . Note that Equation (4.102) is a cubic equation,
possessing a single real root,
that can, in principle, be solved analytically. (See Section 4.17, Exercise 19.) However, a numerical
solution is generally more convenient.
. Note that Equation (4.102) is a cubic equation,
possessing a single real root,
that can, in principle, be solved analytically. (See Section 4.17, Exercise 19.) However, a numerical
solution is generally more convenient.