Next: Exercises Up: Newtonian gravity Previous: Potential outside uniform spheroid
 , radius
, radius 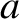 , and negligible cross-sectional area, centered on the origin, and lying in the
, and negligible cross-sectional area, centered on the origin, and lying in the 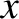 -
-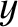 plane.
Let us consider the gravitational potential
plane.
Let us consider the gravitational potential
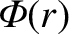 generated by such a ring in the
generated by such a ring in the 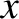 -
-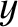 plane
(which corresponds to
plane
(which corresponds to
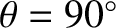 ). It follows, from Section 3.4, that for
). It follows, from Section 3.4, that for 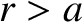 ,
,
![$\displaystyle {\mit\Phi}(r) = - \frac{G\,M}{a}\sum_{n=0,\infty} [P_n(0)]^2\left(\frac{a}{r}\right)^{n+1}.$](img514.png) |
(3.75) |
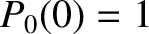 ,
,
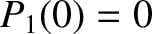 ,
,
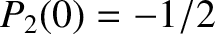 ,
, 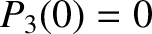 ,
,
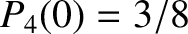 ,
, 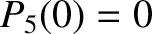 ,
,
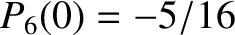 ,
,
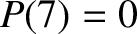 , and
, and
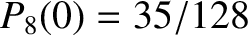 (Abramowitz and Stegun 1965b). Hence,
Likewise, for
(Abramowitz and Stegun 1965b). Hence,
Likewise, for 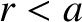 ,
,
![$\displaystyle {\mit\Phi}(r) = - \frac{G\,M}{a}\sum_{n=0,\infty} [P_n(0)]^2\left(\frac{r}{a}\right)^{n},$](img526.png) |
(3.77) |