Next: Expansion of Lagrange planetary Up: Expansion of orbital evolution Previous: Expansion of orbital evolution
Let the first planet have position vector  , mass
, mass  , and the standard osculating elements
, and the standard osculating elements  ,
,
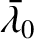 ,
,  ,
,  ,
, 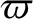 ,
and
,
and
 . (See Section 4.12.) It is convenient to define the alternative elements
. (See Section 4.12.) It is convenient to define the alternative elements
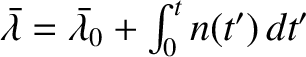 ,
,
 ,
,
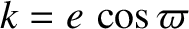 ,
,
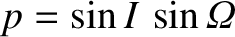 , and
, and
 , where
, where
 is the mean orbital angular velocity,
is the mean orbital angular velocity,
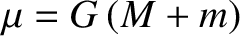 , and
, and  is the solar mass. Thus, the osculating elements of the first planet become
is the solar mass. Thus, the osculating elements of the first planet become  ,
,
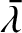 ,
,
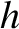 ,
, 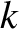 ,
, 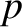 , and
, and  . Let
. Let 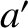 ,
,
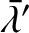 ,
,
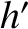 ,
, 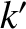 ,
,  , and
, and 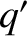 be the corresponding osculating elements of the second planet. Furthermore, let the
second planet have position vector
be the corresponding osculating elements of the second planet. Furthermore, let the
second planet have position vector 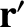 , mass
, mass 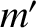 , and mean orbital angular velocity
, and mean orbital angular velocity
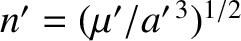 ,
where
,
where
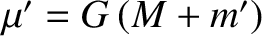 .
.