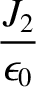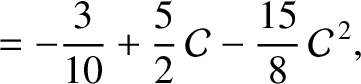To lowest order in  , the moment of inertia of our body about its rotation axis can be written
, the moment of inertia of our body about its rotation axis can be written
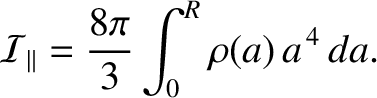 |
(D.43) |
It follows from Equation (D.27) that
![$\displaystyle {\cal I}_\parallel =\frac{8\pi}{9}\int_0^R \left(3\,\bar{\rho}\,a...
...\pi}{9}\left[\bar{\rho}(R)\,R^{\,5}-2\int_0^R\bar{\rho}(a)\,a^{\,4}\,da\right],$](img4397.png) |
(D.44) |
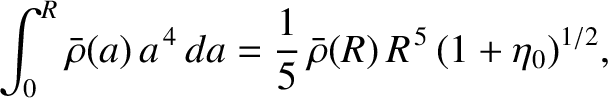 |
(D.45) |
where
 . Hence, we obtain
. Hence, we obtain
![$\displaystyle {\cal I}_\parallel = \frac{8\pi}{9}\,\bar{\rho}(R)\,R^{\,5}\left[1-\frac{2}{5}\,(1+\eta_0)^{1/2}\right].$](img4400.png) |
(D.46) |
It is convenient to define the dimensionless moment of inertia
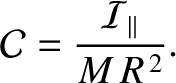 |
(D.47) |
Making use of Equations (D.29) and (D.46), we deduce that
![$\displaystyle {\cal C} =\frac{2}{3}\left[1-\frac{2}{5}\,(1+\eta_0)^{1/2}\right].$](img4402.png) |
(D.48) |
However, Equation (D.31) yields
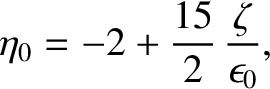 |
(D.49) |
where
 . Hence, we obtain the so-called Darwin-Radau equation (Radau 1885; Darwin 1899),
. Hence, we obtain the so-called Darwin-Radau equation (Radau 1885; Darwin 1899),
![$\displaystyle {\cal C} =\frac{2}{3}\left[1-\frac{2}{5}\left(\frac{15}{2}\,\frac{\zeta}{\epsilon_0}-1\right)^{1/2}\right].$](img4405.png) |
(D.50) |
This equation relates the degree of flattening of an inhomogeneous rotating body to its rotational angular velocity and its
moment of inertia about its rotation axis. The Darwin-Radau equation is only valid if the response of the body to the
centrifugal potential is fluid-like. Recall, also, that the equation was derived under the assumption that the rotation is sufficiently slow that
 and
and 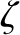 can both be treated as small parameters, and, in particular, that any quantities that are second order, or higher, in these parameters
can be neglected in the analysis. Note, finally, that the derivation of the Darwin-Radau equation depends crucially on the approximation
can both be treated as small parameters, and, in particular, that any quantities that are second order, or higher, in these parameters
can be neglected in the analysis. Note, finally, that the derivation of the Darwin-Radau equation depends crucially on the approximation
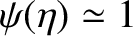 , where
, where
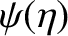 is defined in Equation (D.40).
is defined in Equation (D.40).
For a rotating body in hydrostatic equilibrium (in the co-rotating frame), Equation (6.43) yields
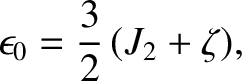 |
(D.51) |
where 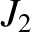 is the body's dimensionless gravitational quadrupole moment. [See Equation (8.86).]
The previous two equations can be combined to give the following alternative versions of the Darwin-Radau equation:
is the body's dimensionless gravitational quadrupole moment. [See Equation (8.86).]
The previous two equations can be combined to give the following alternative versions of the Darwin-Radau equation:
 , the moment of inertia of our body about its rotation axis can be written
, the moment of inertia of our body about its rotation axis can be written
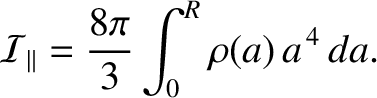
![$\displaystyle {\cal I}_\parallel =\frac{8\pi}{9}\int_0^R \left(3\,\bar{\rho}\,a...
...\pi}{9}\left[\bar{\rho}(R)\,R^{\,5}-2\int_0^R\bar{\rho}(a)\,a^{\,4}\,da\right],$](img4397.png)
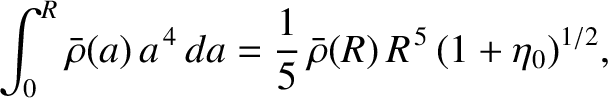
 . Hence, we obtain
It is convenient to define the dimensionless moment of inertia
. Hence, we obtain
It is convenient to define the dimensionless moment of inertia
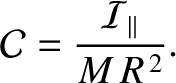
 . Hence, we obtain the so-called Darwin-Radau equation (Radau 1885; Darwin 1899),
. Hence, we obtain the so-called Darwin-Radau equation (Radau 1885; Darwin 1899),
![$\displaystyle {\cal C} =\frac{2}{3}\left[1-\frac{2}{5}\left(\frac{15}{2}\,\frac{\zeta}{\epsilon_0}-1\right)^{1/2}\right].$](img4405.png)
 and
and 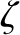 can both be treated as small parameters, and, in particular, that any quantities that are second order, or higher, in these parameters
can be neglected in the analysis. Note, finally, that the derivation of the Darwin-Radau equation depends crucially on the approximation
can both be treated as small parameters, and, in particular, that any quantities that are second order, or higher, in these parameters
can be neglected in the analysis. Note, finally, that the derivation of the Darwin-Radau equation depends crucially on the approximation
 , where
, where
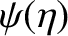 is defined in Equation (D.40).
is defined in Equation (D.40).
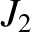 is the body's dimensionless gravitational quadrupole moment. [See Equation (8.86).]
The previous two equations can be combined to give the following alternative versions of the Darwin-Radau equation:
is the body's dimensionless gravitational quadrupole moment. [See Equation (8.86).]
The previous two equations can be combined to give the following alternative versions of the Darwin-Radau equation: