According to the analysis of Section 3.4, we can write
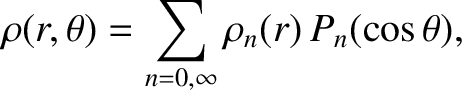 |
(D.8) |
where
 |
(D.9) |
Here, use has been made of Equation (D.5).
Now, to first order in
 , Equation (D.6) can be inverted to give
, Equation (D.6) can be inverted to give
![$\displaystyle a = r\left[1+\frac{2}{3}\,\epsilon(r)\,P_2(\cos\theta)\right].$](img4335.png) |
(D.10) |
Hence, to the same order, Equation (D.9) gives
![$\displaystyle \rho_n(r)= (n+1/2)\int_0^\pi\left[\rho(r)+\frac{2}{3}\,r\,\frac{d...
...}{dr}\,\epsilon(r)\,P_2(\cos\theta)\right]P_n(\cos\theta)\,\sin\theta\,d\theta.$](img4336.png) |
(D.11) |
Making use of Equation (3.42), we deduce that, to first order in
 ,
with all of the other
,
with all of the other  zero.
zero.
The analysis of Section 3.4, combined with the previous two equations, also implies that
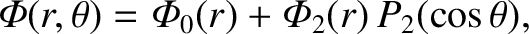 |
(D.14) |
where
![$\displaystyle {\mit\Phi}_0(r)=-4\pi\,G\left[\frac{1}{r}\int_0^r\rho(r')\,r'^{\,2}\,dr'+\int_r^\infty \rho(r')\,r'\,dr'\right],$](img4343.png) |
(D.15) |
and
![$\displaystyle {\mit\Phi}_2(r)=-\frac{8\pi\,G}{15}\left[\frac{1}{r^{\,3}}\int_0^...
...r'^{\,5}\,dr'+r^{\,2}\int_r^\infty
\frac{d\rho}{dr'}\,\epsilon(r')\,dr'\right].$](img4344.png) |
(D.16) |
Now, to first order in
 , we can write
, we can write
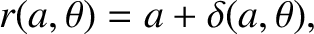 |
(D.17) |
where
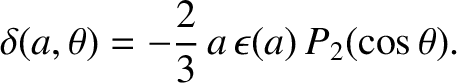 |
(D.18) |
Substitution of Equation (D.17) into Equations (D.15) and (D.16), followed by an expansion to first order in
 , yields
, yields
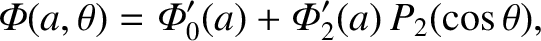 |
(D.19) |
where
![$\displaystyle {\mit\Phi}_0'(a)= -4\pi\,G\left[\frac{1}{a}\int_0^a\rho(a')\,a'^{\,2}\,da'+\int_a^\infty \rho(a')\,a'\,da'\right],$](img4348.png) |
(D.20) |
and
Here, we have integrated the last two terms in curly brackets by parts.
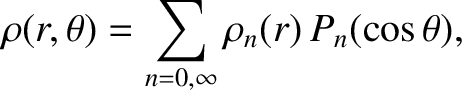
 , Equation (D.6) can be inverted to give
, Equation (D.6) can be inverted to give
![$\displaystyle a = r\left[1+\frac{2}{3}\,\epsilon(r)\,P_2(\cos\theta)\right].$](img4335.png)
![$\displaystyle \rho_n(r)= (n+1/2)\int_0^\pi\left[\rho(r)+\frac{2}{3}\,r\,\frac{d...
...}{dr}\,\epsilon(r)\,P_2(\cos\theta)\right]P_n(\cos\theta)\,\sin\theta\,d\theta.$](img4336.png)
 ,
,

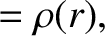
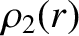
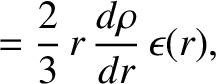
 zero.
zero.
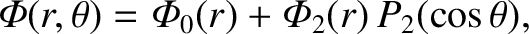
 , we can write
, we can write
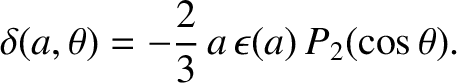
 , yields
, yields
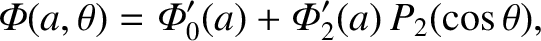
![$\displaystyle {\mit\Phi}_0'(a)= -4\pi\,G\left[\frac{1}{a}\int_0^a\rho(a')\,a'^{\,2}\,da'+\int_a^\infty \rho(a')\,a'\,da'\right],$](img4348.png)
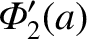
![$\displaystyle =-\frac{8\pi\,G}{3}\left\{\frac{\epsilon(a)}{a}\int_0^a \rho(a')\...
...2}\,da'-\frac{1}{5\,a^{\,3}}\int_0^a \rho(a')\,d[\epsilon(a')\,a'^{\,5}]\right.$](img4350.png)
![$\displaystyle \left.\phantom{=}-\frac{a^{\,2}}{5}\int_a^\infty
\rho(a')\,d[\epsilon(a')]\right\}.$](img4351.png)