Elastic response theory
The interior of the planet is modeled as a uniform, incompressible, elastic solid possessing the isotropic stress-strain relation
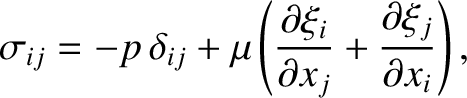 |
(C.21) |
and subject to the incompressibility constraint
Here,
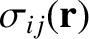 is the stress tensor,
is the stress tensor,
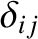 the identity tensor,
the identity tensor,
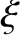
 the elastic displacement,
the elastic displacement,
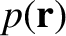 the pressure, and
the pressure, and  the (uniform) rigidity of the material making up the planet (Riley 1974e).
the (uniform) rigidity of the material making up the planet (Riley 1974e).
Force balance inside the planet yields (Love 2011)
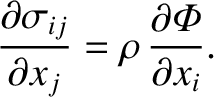 |
(C.23) |
It follows from Equations (C.21) and (C.22) that
Writing
 |
(C.25) |
Equation (C.24) yields
Taking the divergence of the previous equation, and making use of Equation (C.22), we find that
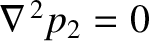 , which implies
that
, which implies
that
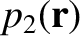 is a solid harmonic (of degree 2). Incidentally,
is a solid harmonic (of degree 2). Incidentally, 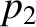 would be zero were the planet in hydrostatic equilibrium.
would be zero were the planet in hydrostatic equilibrium.
It is helpful to define the radial
component of the elastic displacement,
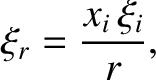 |
(C.28) |
as well as the stress acting (outward) across a constant  surface,
surface,
![$\displaystyle X_i= -\frac{x_j\,\sigma_{ij}}{r} = p\,\frac{x_i}{r} - \frac{\mu}{...
...ial \xi_i}{\partial r}-\xi_i +
\frac{\partial (r\,\xi_r)}{\partial x_i}\right],$](img4275.png) |
(C.29) |
where use has been made of Equation (C.21).
Of course, the radial displacement at 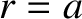 is equivalent to the displacement of the planet's surface:
is equivalent to the displacement of the planet's surface:
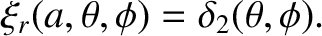 |
(C.30) |
The stress at any point on the surface 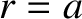 must be entirely radial (because it would be impossible to balance a tangential surface stress), and such as to balance the weight of the column of displaced material directly above the point in question. In other words,
must be entirely radial (because it would be impossible to balance a tangential surface stress), and such as to balance the weight of the column of displaced material directly above the point in question. In other words,
 |
(C.31) |
It follows from Equations (C.18), (C.25), and (C.29) that
where
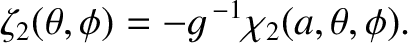 |
(C.34) |
Equations (C.16), (C.26), and (C.32) yield
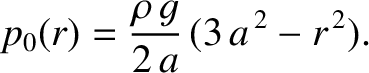 |
(C.35) |
It remains to solve Equations (C.22) and (C.27), subject to the boundary conditions (C.30) and (C.33).
Let us try a solution to Equations (C.22) and (C.27) of the form
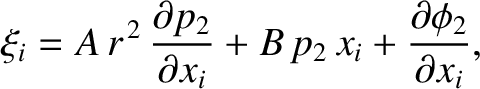 |
(C.36) |
where  and
and 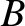 are spatial constants, and
are spatial constants, and
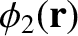 is a solid harmonic of degree 2 (Love 2011). It follows that
is a solid harmonic of degree 2 (Love 2011). It follows that
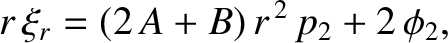 |
(C.37) |
where use has been made of Equation (C.5). Moreover,
where use has been made of Equations (C.5)–(C.7). Thus, the boundary conditions (C.30) and (C.33)
become
respectively. The previous equation implies that
![$\displaystyle \left[(4\,A+B)\,a^{\,2}\,p_2 + 2\,\phi_2\right]_{r=a} = 0.$](img4295.png) |
(C.42) |
Hence, the boundary conditions (C.40) and (C.41) reduce to
respectively.
The expression for 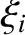 given in Equation (C.36) satisfies Equations (C.22) and (C.27) provided that
given in Equation (C.36) satisfies Equations (C.22) and (C.27) provided that
respectively, where use has been made of Equations (C.5)–(C.7). It follows that
Hence, the boundary conditions (C.43) and (C.44) yield
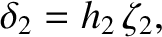 |
(C.49) |
where
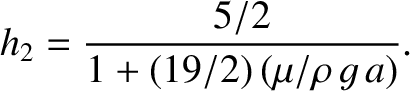 |
(C.50) |
The dimensionless quantity 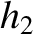 is termed a Love number of degree 2 (Love 2011).
is termed a Love number of degree 2 (Love 2011).
The radial component of the elastic (i.e., non-hydrostatic) stress acting (outward) across the surface 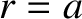 takes the form
takes the form
 |
(C.51) |
where use has been made of Equation (C.33). Equations (C.49) and (C.50) imply that this
stress is related to the radial strain at the surface of the planet according to
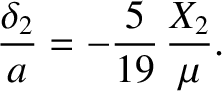 |
(C.52) |
As a specific example, suppose that
where 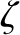 is a dimensionless measure of the strength of the tidal field, and
is a dimensionless measure of the strength of the tidal field, and  is the tidally induced planetary ellipticity.
It follows that
where
is the tidally induced planetary ellipticity.
It follows that
where
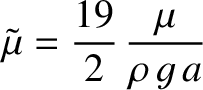 |
(C.58) |
is the planet's effective rigidity.
 is the stress tensor,
is the stress tensor,
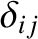 the identity tensor,
the identity tensor,
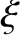
 the elastic displacement,
the elastic displacement,
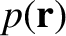 the pressure, and
the pressure, and  the (uniform) rigidity of the material making up the planet (Riley 1974e).
the (uniform) rigidity of the material making up the planet (Riley 1974e).
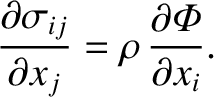
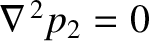 , which implies
that
, which implies
that
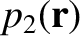 is a solid harmonic (of degree 2). Incidentally,
is a solid harmonic (of degree 2). Incidentally, 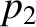 would be zero were the planet in hydrostatic equilibrium.
would be zero were the planet in hydrostatic equilibrium.
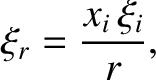
 surface,
where use has been made of Equation (C.21).
Of course, the radial displacement at
surface,
where use has been made of Equation (C.21).
Of course, the radial displacement at 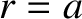 is equivalent to the displacement of the planet's surface:
The stress at any point on the surface
is equivalent to the displacement of the planet's surface:
The stress at any point on the surface 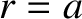 must be entirely radial (because it would be impossible to balance a tangential surface stress), and such as to balance the weight of the column of displaced material directly above the point in question. In other words,
It follows from Equations (C.18), (C.25), and (C.29) that
where
Equations (C.16), (C.26), and (C.32) yield
must be entirely radial (because it would be impossible to balance a tangential surface stress), and such as to balance the weight of the column of displaced material directly above the point in question. In other words,
It follows from Equations (C.18), (C.25), and (C.29) that
where
Equations (C.16), (C.26), and (C.32) yield
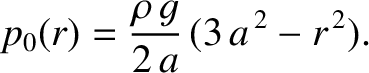
 and
and 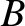 are spatial constants, and
are spatial constants, and
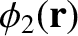 is a solid harmonic of degree 2 (Love 2011). It follows that
is a solid harmonic of degree 2 (Love 2011). It follows that
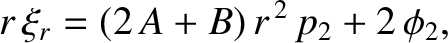
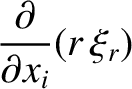
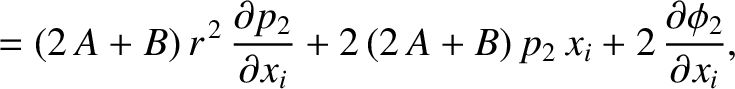
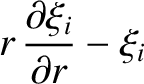
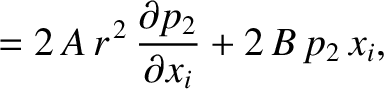
![$\displaystyle \left[(4\,A+B)\,a^{\,2}\,p_2 + 2\,\phi_2\right]_{r=a} = 0.$](img4295.png)
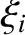 given in Equation (C.36) satisfies Equations (C.22) and (C.27) provided that
given in Equation (C.36) satisfies Equations (C.22) and (C.27) provided that
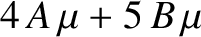
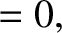
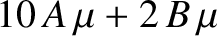
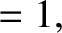
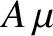
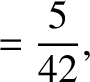
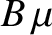
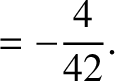
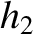 is termed a Love number of degree 2 (Love 2011).
is termed a Love number of degree 2 (Love 2011).
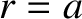 takes the form
takes the form

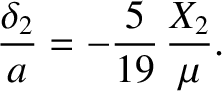
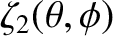
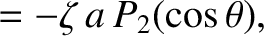
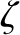 is a dimensionless measure of the strength of the tidal field, and
is a dimensionless measure of the strength of the tidal field, and  is the tidally induced planetary ellipticity.
It follows that
where
is the planet's effective rigidity.
is the tidally induced planetary ellipticity.
It follows that
where
is the planet's effective rigidity.