Next: Precession Up: Useful mathematics Previous: Conservative fields
 ,
,  ,
,  .
Suppose that we transform to a new coordinate system,
.
Suppose that we transform to a new coordinate system, 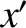 ,
, 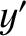 ,
, 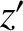 , that is obtained
from the
, that is obtained
from the  ,
,  ,
,  system by
rotating the coordinate axes through an angle
system by
rotating the coordinate axes through an angle
 about the
about the  -axis. See Figure A.1.
Let the coordinates of a general point
-axis. See Figure A.1.
Let the coordinates of a general point 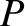 be
be
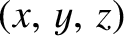 in the first coordinate system, and
in the first coordinate system, and
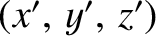 in the second. According to simple trigonometry, these two sets of coordinates are related to one another via the transformation:
When expressed in matrix form, this transformation becomes
The reverse transformation is accomplished by rotating the coordinate axes through an angle
in the second. According to simple trigonometry, these two sets of coordinates are related to one another via the transformation:
When expressed in matrix form, this transformation becomes
The reverse transformation is accomplished by rotating the coordinate axes through an angle 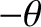 about
the
about
the 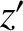 -axis:
It follows that the matrix appearing in Equation (A.89) is the inverse of that appearing in Equation (A.90),
and vice versa.
However, because these two matrices are clearly also the transposes of one another, we deduce that both matrices are unitary.
In fact, it is easily demonstrated that all rotation matrices must be unitary; otherwise they would not
preserve the lengths of the vectors on which they act.
-axis:
It follows that the matrix appearing in Equation (A.89) is the inverse of that appearing in Equation (A.90),
and vice versa.
However, because these two matrices are clearly also the transposes of one another, we deduce that both matrices are unitary.
In fact, it is easily demonstrated that all rotation matrices must be unitary; otherwise they would not
preserve the lengths of the vectors on which they act.
A rotation through an angle  about the
about the 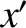 -axis transforms the
-axis transforms the 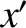 ,
, 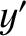 ,
, 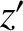 coordinate system into the
coordinate system into the 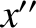 ,
,  ,
, 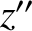 system, where, by analogy with the previous analysis,
system, where, by analogy with the previous analysis,
 about the
about the  -axis, followed by a rotation through an angle
-axis, followed by a rotation through an angle  about the
about the 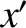 -axis, transforms the
-axis, transforms the  ,
,  ,
,  coordinate system into the
coordinate system into the 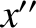 ,
,  ,
, 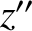 system, where
system, where
![$\displaystyle \left(\begin{array}{c}x''\\ [0.5ex]y''\\ [0.5ex]z''\end{array}\ri...
...d{array}\right)\left(\begin{array}{c}x\\ [0.5ex]y\\ [0.5ex]z\end{array}\right).$](img3961.png) |
(A.92) |