Next: Newtonian gravity Up: Newtonian mechanics Previous: Two-body problem
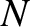 point particles. Let
point particles. Let 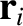 be the position vector of the
be the position vector of the  th particle, and
let
th particle, and
let 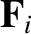 be the external force acting on this particle. Any internal forces are
assumed to be central in nature. The resultant force and torque (about the origin) acting on the system are
be the external force acting on this particle. Any internal forces are
assumed to be central in nature. The resultant force and torque (about the origin) acting on the system are
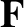 |
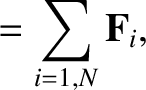 |
|
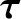 |
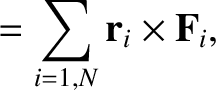 |
 satisfies
satisfies
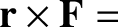
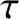

 is arbitrary. This straight line is known as the line of action of the
resultant force.
is arbitrary. This straight line is known as the line of action of the
resultant force.
 and
and 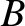 . Let
. Let
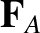 be
the resultant force acting on
be
the resultant force acting on  due to
due to 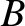 , and let
, and let
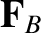 be the resultant force acting on
be the resultant force acting on 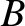 due to
due to  . Demonstrate that
. Demonstrate that
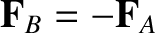 , and that both forces have the same
line of action.
, and that both forces have the same
line of action.
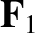 and
and 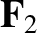 .
Show that these forces can be only replaced by a single equivalent force,
.
Show that these forces can be only replaced by a single equivalent force,
 ,
provided:
,
provided:
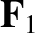 and
and 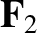 are parallel (or antiparallel). In this case, the line of action of
are parallel (or antiparallel). In this case, the line of action of 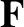 is parallel to those of
is parallel to those of 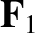 and
and 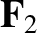 .
.
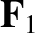 and
and 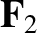 are not parallel (or antiparallel), but their lines of action cross at a point (with one proviso).
In this case, the line of action of
are not parallel (or antiparallel), but their lines of action cross at a point (with one proviso).
In this case, the line of action of 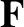 passes through the crossing point.
passes through the crossing point.
 ,
, 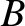 , and
, and  , where
, where
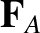 is
the resultant force acting on
is
the resultant force acting on  (due to
(due to 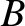 and
and  ),
),
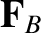 is the resultant force acting on
is the resultant force acting on 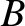 , and
, and
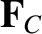 is the resultant force acting on
is the resultant force acting on  , then
, then
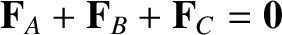 and the
forces either all have parallel lines of action or have lines of action that cross at a common point.
and the
forces either all have parallel lines of action or have lines of action that cross at a common point.
 moves in one dimension and has an instantaneous displacement
moves in one dimension and has an instantaneous displacement  . The particle is
released at rest from
. The particle is
released at rest from  ,
subject to the force
,
subject to the force
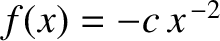 , where
, where  ,
,  . Demonstrate that the time needed
for the particle to reach
. Demonstrate that the time needed
for the particle to reach 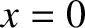 is
is
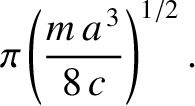
 moves in one dimension and has an instantaneous displacement
moves in one dimension and has an instantaneous displacement  .
The particle is released at rest from
.
The particle is released at rest from  , subject to the force
, subject to the force
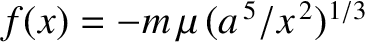 , where
, where  . Show that
the particle will reach the origin with a speed
. Show that
the particle will reach the origin with a speed
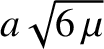 after a time
after a time
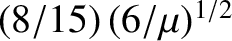 has elapsed.
(Modified from Smart 1951.)
has elapsed.
(Modified from Smart 1951.)
 .
The particle is released at rest from
.
The particle is released at rest from  and accelerates such that
and accelerates such that
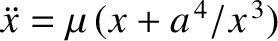 , where
, where  , and
, and
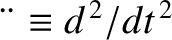 . Show that
the particle will reach the origin after a time
. Show that
the particle will reach the origin after a time
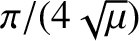 has elapsed, and that its speed is then infinite. (Modified from Smart 1951.)
has elapsed, and that its speed is then infinite. (Modified from Smart 1951.)
 , moving in one dimension with an initial (i.e., at
, moving in one dimension with an initial (i.e., at 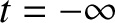 ) velocity
) velocity  , is subject to a force
, is subject to a force
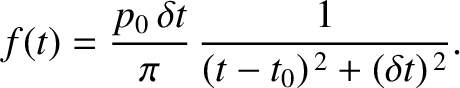
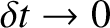 the motion approaches motion
at constant velocity with an abrupt change in velocity, by an amount
the motion approaches motion
at constant velocity with an abrupt change in velocity, by an amount 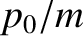 , at
, at 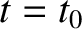 .
.
 moving in one dimension is subject to a force
moving in one dimension is subject to a force
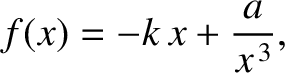
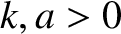 . Find the potential energy,
. Find the potential energy, 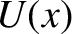 . Find the equilibrium points. Are they stable or unstable?
Determine the angular frequency of small-amplitude oscillations about any stable equilibrium points.
. Find the equilibrium points. Are they stable or unstable?
Determine the angular frequency of small-amplitude oscillations about any stable equilibrium points.
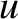 and
and 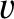 at displacements
at displacements
 and
and 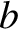 , respectively, from its mean position. Show that the period of the motion is
, respectively, from its mean position. Show that the period of the motion is
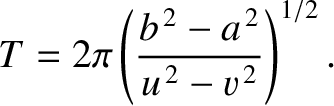
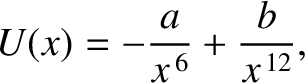
 is the distance between the atoms, and
is the distance between the atoms, and  are positive constants. Find the force.
are positive constants. Find the force.
 , moves in a
straight line, find the equilibrium distance and the period of small oscillations about the
equilibrium position.
, moves in a
straight line, find the equilibrium distance and the period of small oscillations about the
equilibrium position.
 , and move in a straight line, find the equilibrium distance and the period of small oscillations about the
equilibrium position.
, and move in a straight line, find the equilibrium distance and the period of small oscillations about the
equilibrium position.
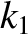 and
and  , respectively, and are used in a vertical
orientation to support an object of mass
, respectively, and are used in a vertical
orientation to support an object of mass  . Show that the angular frequency of oscillation
is
. Show that the angular frequency of oscillation
is
![$[(k_1+k_2)/m]^{1/2}$](img318.png) if the springs are connected in parallel, and
if the springs are connected in parallel, and
![$[k_1\,k_2/(k_1+k_2)\,m]^{1/2}$](img319.png) if the springs are connected in series.
if the springs are connected in series.
 and mass density
and mass density 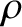 floats in a liquid
of density
floats in a liquid
of density 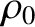 (where
(where
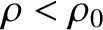 ), and at equilibrium displaces a volume
), and at equilibrium displaces a volume 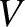 . Show
that the period of small oscillations about the equilibrium position is
. Show
that the period of small oscillations about the equilibrium position is

 executes one-dimensional simple harmonic oscillation under the action of a
conservative force such that its instantaneous displacement is
executes one-dimensional simple harmonic oscillation under the action of a
conservative force such that its instantaneous displacement is
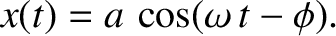
 ,
, 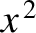 ,
, 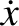 , and
, and
 over a single cycle of the
oscillation. Here,
over a single cycle of the
oscillation. Here,
 . Find the average values of the kinetic and potential energies of the
particle over a single cycle of the oscillation.
. Find the average values of the kinetic and potential energies of the
particle over a single cycle of the oscillation.
 |
 |
|
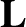 |
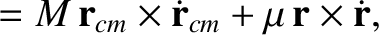 |
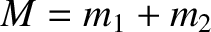 , and
, and
 .
.
 , demonstrate that the
total energy of the system is written
, demonstrate that the
total energy of the system is written
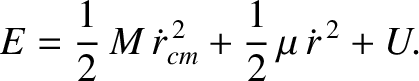
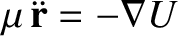 , that
, that  is constant in time.
is constant in time.
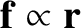 , demonstrate, from the
equation of motion,
, demonstrate, from the
equation of motion,
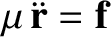 , that
, that 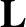 is constant in time.
is constant in time.