Next: Useful mathematics Up: Lunar motion Previous: Historical note
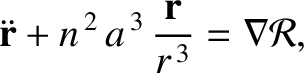
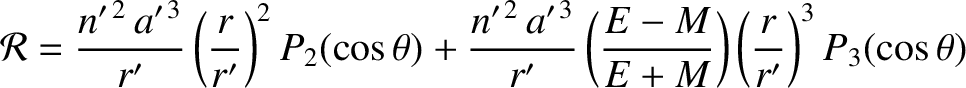
 represents the position of the Moon relative to the Earth,
represents the position of the Moon relative to the Earth,
 the position of the Sun relative to the Earth–Moon barycenter,
the position of the Sun relative to the Earth–Moon barycenter,  the angle subtended between
the angle subtended between  and
and  ,
,  the
mean orbital angular velocity of the Moon around the Earth,
the
mean orbital angular velocity of the Moon around the Earth, 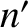 the mean (apparent) orbital angular velocity of the Sun around the Earth–Moon barycenter,
the mean (apparent) orbital angular velocity of the Sun around the Earth–Moon barycenter,
 the mean radius of the former orbit,
the mean radius of the former orbit, 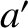 the mean radius of the latter orbit,
the mean radius of the latter orbit,  the mass of the Earth, and
the mass of the Earth, and  the mass of the moon.
the mass of the moon.
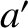 , and that of the
Moon and the Earth about the barycenter as a circle of major radius
, and that of the
Moon and the Earth about the barycenter as a circle of major radius  , and then averaging over the motions of the Moon and the Earth,
show that Equation (11.34) reduces to
, and then averaging over the motions of the Moon and the Earth,
show that Equation (11.34) reduces to

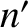 is the mean orbital angular velocity of the barycenter,
is the mean orbital angular velocity of the barycenter,
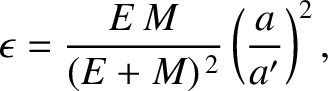
 is the mass of the Earth, and
is the mass of the Earth, and  is the mass of the Moon. Hence, deduce that the combined disturbing action of the Earth and the
Moon causes an additional precession of the perihelion of the barycenter's orbit at the rate
is the mass of the Moon. Hence, deduce that the combined disturbing action of the Earth and the
Moon causes an additional precession of the perihelion of the barycenter's orbit at the rate
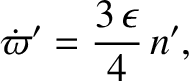
 arc seconds per (Julian) century. Note that this precession rate is much less than that caused by the other planets in the solar system. (See Section 5.4.)
arc seconds per (Julian) century. Note that this precession rate is much less than that caused by the other planets in the solar system. (See Section 5.4.)
 and
and
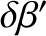 be the associated displacements of the Sun, in ecliptic longitude and latitude, respectively, with
respect to a Keplerian orbit. Demonstrate that
be the associated displacements of the Sun, in ecliptic longitude and latitude, respectively, with
respect to a Keplerian orbit. Demonstrate that
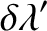 |
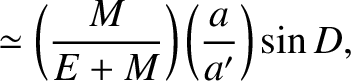 |
|
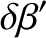 |
 |
 is the mass of the Moon,
is the mass of the Moon,  the mass of the Earth,
the mass of the Earth,  the major radius of the lunar orbit,
the major radius of the lunar orbit,
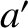 the major radius of the barycenter's orbit,
the major radius of the barycenter's orbit,  the inclination of the lunar orbit to the ecliptic plane,
the inclination of the lunar orbit to the ecliptic plane, 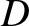 the mean elongation of the Moon from the Earth, and
the mean elongation of the Moon from the Earth, and
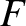 the lunar mean argument of latitude. Show that
the lunar mean argument of latitude. Show that
 and
and
 .
.
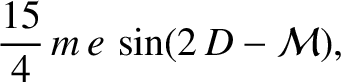
 , of the lunar orbit, and the mean longitude,
, of the lunar orbit, and the mean longitude,  , of the lunar perigee: in other words,
, of the lunar perigee: in other words,
![$e\rightarrow
e\,[1-(15/8)\,m\,\cos (2\, D)]$](img3688.png) and
and
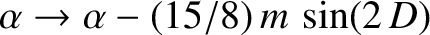 . Likewise, show that the lowest-order evection term,
. Likewise, show that the lowest-order evection term,
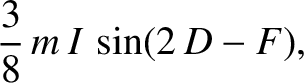
 , of the lunar orbit, and the mean longitude,
, of the lunar orbit, and the mean longitude,  , of the lunar ascending node: in other words,
, of the lunar ascending node: in other words,
![$I\rightarrow
I\,[1-(3/8)\,m\,\cos (2\, D)]$](img3691.png) and
and
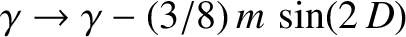 .
.
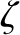 ; that is,
; that is,
 , where
, where 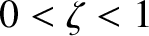 . Assuming that the masses of the Earth and Sun, and the major radius of the terrestrial
orbit, remain constant, demonstrate that the parameter
. Assuming that the masses of the Earth and Sun, and the major radius of the terrestrial
orbit, remain constant, demonstrate that the parameter  , which measures the lowest-order perturbing influence of the Sun on
the lunar orbit, would be reduced by a factor
, which measures the lowest-order perturbing influence of the Sun on
the lunar orbit, would be reduced by a factor
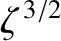 ; in other words,
; in other words,
 . Given that
. Given that 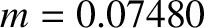 for
the true lunar orbit, how small would
for
the true lunar orbit, how small would 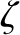 have to be before the (theoretical) precession rate of the lunar
perigee became equal to the regression rate of the ascending node to within
have to be before the (theoretical) precession rate of the lunar
perigee became equal to the regression rate of the ascending node to within  percent? What is the corresponding major radius
of the lunar orbit in units of mean Earth radii? (The true major radius of the lunar orbit is
percent? What is the corresponding major radius
of the lunar orbit in units of mean Earth radii? (The true major radius of the lunar orbit is 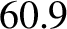 mean Earth radii.)
mean Earth radii.)
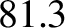 times that of the Moon, and the major radius of the lunar orbit is
times that of the Moon, and the major radius of the lunar orbit is 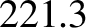 times the lunar radius,
estimate the precession period of the satellite orbit's perilune (i.e., its point of closest approach to the Moon) in months due to
the perturbing influence of the Earth. Likewise, estimate the regression rate of the satellite orbit's ascending node (with respect to the
plane of the lunar orbit) in months. (Assume that the Moon is a perfect sphere.)
times the lunar radius,
estimate the precession period of the satellite orbit's perilune (i.e., its point of closest approach to the Moon) in months due to
the perturbing influence of the Earth. Likewise, estimate the regression rate of the satellite orbit's ascending node (with respect to the
plane of the lunar orbit) in months. (Assume that the Moon is a perfect sphere.)
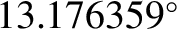 per day and
per day and
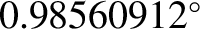 per day, respectively. However, the vernal equinox regresses in such a manner that, on average, it completes a full
circuit every
per day, respectively. However, the vernal equinox regresses in such a manner that, on average, it completes a full
circuit every 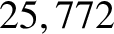 years. Furthermore, the lunar perigee precesses in such a manner that, on average, it completes a full circuit every
years. Furthermore, the lunar perigee precesses in such a manner that, on average, it completes a full circuit every 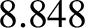 years, whereas the lunar ascending mode regresses in such a manner that, on average, it completes a full circuit every
years, whereas the lunar ascending mode regresses in such a manner that, on average, it completes a full circuit every 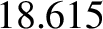 years (Yoder 1995). A sidereal month is the mean period of the Moon's orbit with respect to the fixed stars, a tropical month is the
mean time required for the Moon's ecliptic longitude (with respect to the true vernal equinox) to increase by
years (Yoder 1995). A sidereal month is the mean period of the Moon's orbit with respect to the fixed stars, a tropical month is the
mean time required for the Moon's ecliptic longitude (with respect to the true vernal equinox) to increase by  , a
synodic month is the mean period between successive new moons, an anomalistic month is the mean
period between successive passages of the Moon through its perigee, and a draconic month is the
mean period between successive passages of the Moon through its ascending node. Use the preceding information to
demonstrate than the lengths of a sidereal, tropical, synodic, anomalistic, and draconic month are
, a
synodic month is the mean period between successive new moons, an anomalistic month is the mean
period between successive passages of the Moon through its perigee, and a draconic month is the
mean period between successive passages of the Moon through its ascending node. Use the preceding information to
demonstrate than the lengths of a sidereal, tropical, synodic, anomalistic, and draconic month are 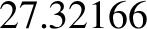 ,
, 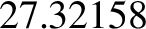 ,
,
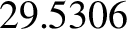 ,
, 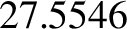 , and
, and 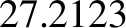 days, respectively.
days, respectively.
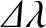 |
![$\displaystyle \simeq (n-n')\,t + 2\,e\,\sin[(n-n_p)\,t],$](img3711.png) |
|
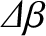 |
![$\displaystyle \simeq I\,\sin[(n-n_n)\,t],$](img3713.png) |
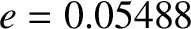 and
and 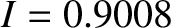 radians. Here,
radians. Here,  and
and 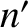 are the mean geocentric orbital angular velocities of the Moon and Sun,
respectively,
are the mean geocentric orbital angular velocities of the Moon and Sun,
respectively, 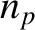 is the mean orbital angular velocity of the lunar perigee, and
is the mean orbital angular velocity of the lunar perigee, and 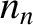 is the mean orbital angular
velocity of the lunar ascending node. Note that
is the mean orbital angular
velocity of the lunar ascending node. Note that
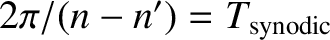 ,
,
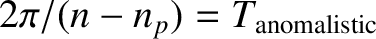 ,
and
,
and
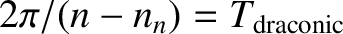 , where
, where
 ,
,
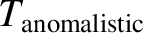 , and
, and
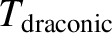 are the
lengths of a synodic, anomalistic, and draconic month, respectively. At
are the
lengths of a synodic, anomalistic, and draconic month, respectively. At 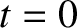 , we have
, we have
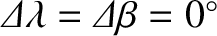 .
In other words, at
.
In other words, at 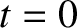 , the Moon and Sun have exactly the same geocentric ecliptic longitudes and latitudes, which implies that
a solar eclipse occurs at this time. Suppose we can find some time period
, the Moon and Sun have exactly the same geocentric ecliptic longitudes and latitudes, which implies that
a solar eclipse occurs at this time. Suppose we can find some time period 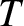 that satisfies
that satisfies
 , where
, where 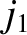 ,
, 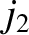 ,
,  are positive integers. Demonstrate that
are positive integers. Demonstrate that
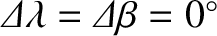 at
at
 . Thus, if the period
. Thus, if the period 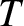 , which is known as the saros, existed then solar (and lunar) eclipses would occur
in infinite sequences spaced
, which is known as the saros, existed then solar (and lunar) eclipses would occur
in infinite sequences spaced 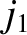 synodic months apart (Roy 2005). Show that for
synodic months apart (Roy 2005). Show that for
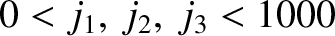 , the
closest approximation to the saros is obtained when
, the
closest approximation to the saros is obtained when 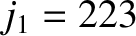 ,
, 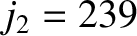 , and
, and 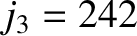 . Demonstrate that
if
. Demonstrate that
if
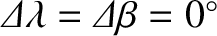 at
at 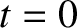 (i.e., if there is a solar eclipse at
(i.e., if there is a solar eclipse at 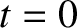 ) then, exactly
) then, exactly  synodic months
later,
synodic months
later,
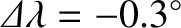 and
and
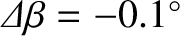 . It turns out that these values of
. It turns out that these values of
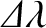 and
and
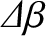 are sufficiently small that the eclipse reoccurs. In fact,
because
are sufficiently small that the eclipse reoccurs. In fact,
because  synodic months almost satisfies the saros condition,
solar (and lunar) eclipses occur in series of about 70 eclipses spaced
synodic months almost satisfies the saros condition,
solar (and lunar) eclipses occur in series of about 70 eclipses spaced  synodic months, or 18 years and 11 days, apart.
synodic months, or 18 years and 11 days, apart.
 -,
-,  -, and
-, and  -axes be the lunar principal axes of rotation passing through the lunar
center of mass. Because the Moon is not quite spherically symmetric, its
principal moments of inertia are not exactly equal to one another. Let us label the principal axes such that
-axes be the lunar principal axes of rotation passing through the lunar
center of mass. Because the Moon is not quite spherically symmetric, its
principal moments of inertia are not exactly equal to one another. Let us label the principal axes such that
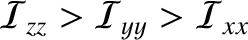 .
To a first approximation, the Moon is spinning about the
.
To a first approximation, the Moon is spinning about the  -axis, which is orientated normal to its orbital plane. Moreover,
the Moon spins in such a manner that the
-axis, which is orientated normal to its orbital plane. Moreover,
the Moon spins in such a manner that the  -axis always points approximately in the direction of the Earth. Let
-axis always points approximately in the direction of the Earth. Let 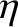 be the (small) angle subtended between the
be the (small) angle subtended between the  -axis and the line joining the centers of the Moon and the Earth.
A slight generalization of the analysis in Section 8.11 reveals that
-axis and the line joining the centers of the Moon and the Earth.
A slight generalization of the analysis in Section 8.11 reveals that

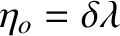 and
and 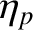 are the Moon's optical and physical libration (in ecliptic longitude), respectively,
are the Moon's optical and physical libration (in ecliptic longitude), respectively,
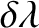 is defined in Equation (11.104), and
is defined in Equation (11.104), and
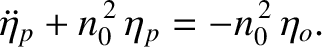
![$n_0= [3\,({\cal I}_{yy}-{\cal I}_{xx})/{\cal I}_{zz}]^{1/2}\,n = 0.3446^\circ$](img3741.png) per day is the Moon's free libration rate,
whereas
per day is the Moon's free libration rate,
whereas
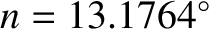 per day is the lunar mean sidereal orbital angular velocity.
per day is the lunar mean sidereal orbital angular velocity.
We can write
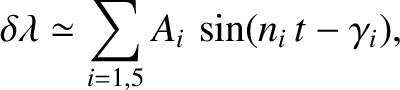
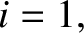
 ,
,  ,
, 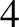 , and
, and 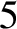 terms correspond to the major inequality, the reduction to the ecliptic,
variation, evection, and the annual inequality, respectively. Furthermore,
terms correspond to the major inequality, the reduction to the ecliptic,
variation, evection, and the annual inequality, respectively. Furthermore,
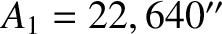 ,
, 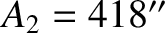 ,
,
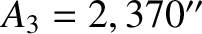 ,
,
 ,
, 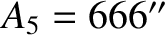 , and
, and  ,
,
 ,
,
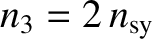 ,
,
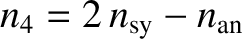 ,
,
 . Here,
. Here,
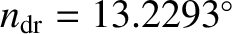 per day,
per day,
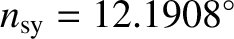 per day,
per day,
 per day,
are the lunar mean draconic, synodic, and anomalistic orbital angular
velocities, respectively, and
per day,
are the lunar mean draconic, synodic, and anomalistic orbital angular
velocities, respectively, and
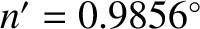 per day is the Earth's mean sidereal orbital angular velocity.
Demonstrate that
per day is the Earth's mean sidereal orbital angular velocity.
Demonstrate that
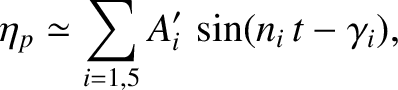
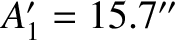 ,
,
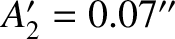 ,
,
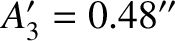 ,
,
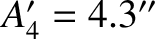 , and
, and
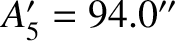 are
the forced libration amplitudes associated with the major inequality, reduction to the ecliptic, variation,
evection, and the annual inequality, respectively. [The observed values of
are
the forced libration amplitudes associated with the major inequality, reduction to the ecliptic, variation,
evection, and the annual inequality, respectively. [The observed values of 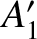 ,
, 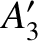 ,
, 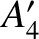 , and
, and
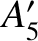 are
are 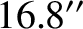 ,
, 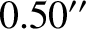 ,
, 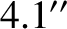 , and
, and 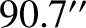 , respectively.
, respectively. 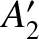 is too small to
measure. (Meeus 2005).]
is too small to
measure. (Meeus 2005).]