Next: Summary of results Up: Lunar motion Previous: Evection in latitude
According to Equation (11.153),
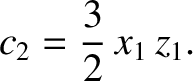 |
(11.321) |
According to Equation (11.154),
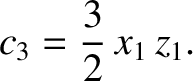 |
(11.323) |
According to Equation (11.127),
 |
(11.325) |
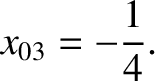 |
(11.326) |
Finally, according to Equations (11.130) and (11.142),
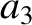 |
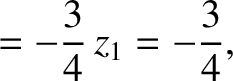 |
(11.327) |
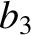 |
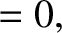 |
(11.328) |
It follows from Equations (11.122)–(11.124), (11.159), (11.162), (11.174), (11.185), and (11.186), as well as the previous expressions for
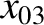 ,
, 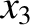 ,
,  ,
, 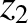 ,
and
,
and 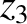 , that the net perturbation to the lunar orbit
due to the remaining terms in the solution of the lunar equations of motion is
, that the net perturbation to the lunar orbit
due to the remaining terms in the solution of the lunar equations of motion is
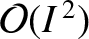 and
and
 .
.
All of the terms on the right-hand sides of Equations (11.332) and (11.333) are Keplerian in origin (i.e., they are independent of the perturbing influence of the Sun). The term on the right-hand side of Equation (11.332) is due to the slight inclination of the lunar orbit to the ecliptic plane, and is known as the reduction to the ecliptic.