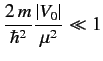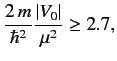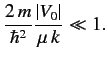

Next: Partial Waves
Up: Scattering Theory
Previous: Fundamental Equations
Equation (938) is not particularly useful, as it stands, because the
quantity
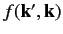 depends on the unknown ket
depends on the unknown ket
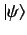 .
Recall that
.
Recall that
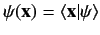 is the solution of the integral equation
is the solution of the integral equation
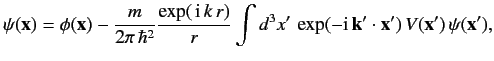 |
(939) |
where
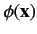 is the wavefunction of the incident state.
According to the above equation, the total wavefunction is a superposition
of the incident wavefunction and lots of spherical waves emitted from
the scattering region. The strength of the spherical wave emitted at
a given point is proportional to the local value of the scattering
potential,
is the wavefunction of the incident state.
According to the above equation, the total wavefunction is a superposition
of the incident wavefunction and lots of spherical waves emitted from
the scattering region. The strength of the spherical wave emitted at
a given point is proportional to the local value of the scattering
potential, 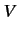 , as well as the local value of the wavefunction,
, as well as the local value of the wavefunction, 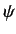 .
.
Suppose that the scattering is not particularly strong. In this case, it is
reasonable to suppose that the total wavefunction,
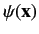 , does
not differ substantially from the incident wavefunction,
, does
not differ substantially from the incident wavefunction,
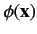 .
Thus, we can obtain an expression for
.
Thus, we can obtain an expression for
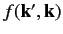 by making
the substitution
by making
the substitution
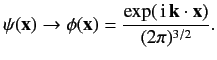 |
(940) |
This is called the Born approximation.
The Born approximation yields
![$\displaystyle f({\bf k}', {\bf k}) \simeq - \frac{m}{2\pi\, \hbar^2} \int d^3 x'\,\exp\left[\, {\rm i}\, ({\bf k} - {\bf k}')\cdot {\bf x}'\right] V({\bf x}').$](img2192.png) |
(941) |
Thus,
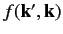 is proportional to the Fourier transform
of the scattering potential
is proportional to the Fourier transform
of the scattering potential
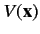 with respect to the wavevector
with respect to the wavevector
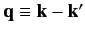 .
.
For a spherically symmetric potential,
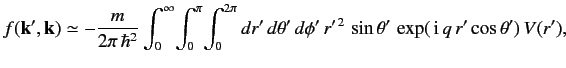 |
(942) |
giving
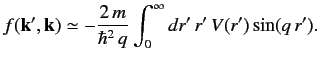 |
(943) |
Note that
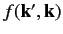 is just a function of
is just a function of 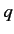 for a
spherically symmetric potential.
It is easily demonstrated that
for a
spherically symmetric potential.
It is easily demonstrated that
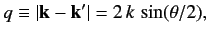 |
(944) |
where 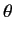 is the angle subtended between the vectors
is the angle subtended between the vectors
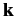 and
and 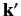 . In other words,
. In other words, 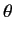 is the angle of
scattering. Recall that the
vectors
is the angle of
scattering. Recall that the
vectors 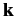 and
and 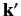 have the same length, as a consequence of energy conservation.
have the same length, as a consequence of energy conservation.
Consider scattering by a Yukawa potential
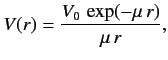 |
(945) |
where 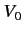 is a constant, and
is a constant, and 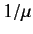 measures the ``range'' of the
potential. It follows from Equation (943) that
measures the ``range'' of the
potential. It follows from Equation (943) that
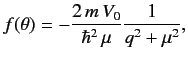 |
(946) |
because
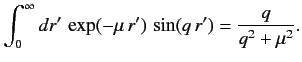 |
(947) |
Thus, in the Born approximation, the differential cross-section
for scattering by a Yukawa potential is
![$\displaystyle \frac{d\sigma}{d {\mit\Omega}} \simeq \left(\frac{2\,m \,V_0}{ \hbar^2\,\mu}\right)^2 \frac{1}{[4\,k^2\,\sin^2(\theta/2) + \mu^2]^{\,2}}.$](img2202.png) |
(948) |
The Yukawa potential reduces to the familiar Coulomb potential as
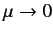 , provided that
, provided that
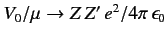 . In this limit, the Born differential cross-section becomes
. In this limit, the Born differential cross-section becomes
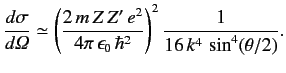 |
(949) |
Recall that 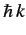 is equivalent to
is equivalent to 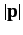 , so the above
equation can be rewritten
, so the above
equation can be rewritten
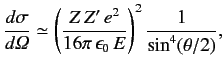 |
(950) |
where
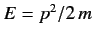 is the kinetic energy of the incident particles.
Equation (950) is identical to the classical Rutherford scattering cross-section formula.
is the kinetic energy of the incident particles.
Equation (950) is identical to the classical Rutherford scattering cross-section formula.
The Born approximation is valid provided that
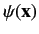 is
not too different from
is
not too different from
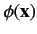 in the scattering region.
It follows, from Equation (922), that the condition for
in the scattering region.
It follows, from Equation (922), that the condition for
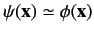 in the vicinity of
in the vicinity of
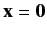 is
is
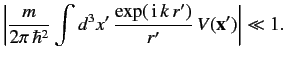 |
(951) |
Consider the special case of the Yukawa potential. At low energies,
(i.e., 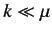 ) we can replace
) we can replace
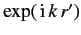 by unity,
giving
by unity,
giving
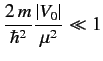 |
(952) |
as the condition for the validity of the Born approximation.
The condition for the Yukawa potential to develop a bound state
is
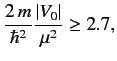 |
(953) |
where 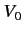 is negative. Thus, if the potential is strong enough to
form a bound state then the Born approximation is likely to break
down. In the high-
is negative. Thus, if the potential is strong enough to
form a bound state then the Born approximation is likely to break
down. In the high-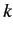 limit, Equation (951) yields
limit, Equation (951) yields
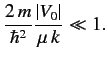 |
(954) |
This inequality becomes progressively easier to satisfy as 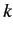 increases,
implying that the Born approximation is more accurate at high
incident particle energies.
increases,
implying that the Born approximation is more accurate at high
incident particle energies.


Next: Partial Waves
Up: Scattering Theory
Previous: Fundamental Equations
Richard Fitzpatrick
2013-04-08
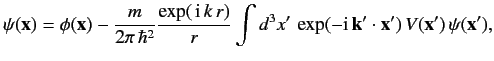
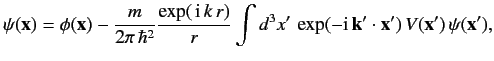
![]() , does
not differ substantially from the incident wavefunction,
, does
not differ substantially from the incident wavefunction,
![]() .
Thus, we can obtain an expression for
.
Thus, we can obtain an expression for
![]() by making
the substitution
by making
the substitution
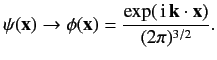
![$\displaystyle f({\bf k}', {\bf k}) \simeq - \frac{m}{2\pi\, \hbar^2} \int d^3 x'\,\exp\left[\, {\rm i}\, ({\bf k} - {\bf k}')\cdot {\bf x}'\right] V({\bf x}').$](img2192.png)
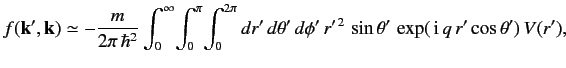
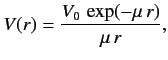
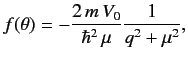
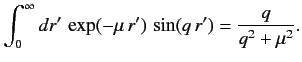
![$\displaystyle \frac{d\sigma}{d {\mit\Omega}} \simeq \left(\frac{2\,m \,V_0}{ \hbar^2\,\mu}\right)^2 \frac{1}{[4\,k^2\,\sin^2(\theta/2) + \mu^2]^{\,2}}.$](img2202.png)
![]() , provided that
, provided that
![]() . In this limit, the Born differential cross-section becomes
. In this limit, the Born differential cross-section becomes
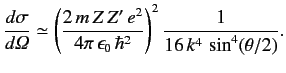
![]() is
not too different from
is
not too different from
![]() in the scattering region.
It follows, from Equation (922), that the condition for
in the scattering region.
It follows, from Equation (922), that the condition for
![]() in the vicinity of
in the vicinity of
![]() is
is