

Next: Addition of Angular Momentum
Up: Spin Angular Momentum
Previous: Spin Greater Than One-Half
- Demonstrate that the operators defined in Equations (427)-(429) are Hermitian, and
satisfy
the commutation relations (417).
- Prove the Baker-Hausdorff lemma, (447).
- Find the Pauli representations of the normalized eigenstates of
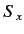 and
and 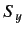 for
a spin-
for
a spin-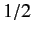 particle.
particle.
- Suppose that a spin-
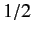 particle
has a spin vector that lies in the
particle
has a spin vector that lies in the 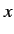 -
-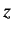 plane, making an
angle
plane, making an
angle 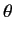 with the
with the 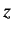 -axis. Demonstrate that a measurement of
-axis. Demonstrate that a measurement of 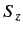 yields
yields 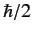 with probability
with probability
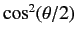 , and
, and 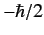 with probability
with probability
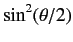 .
.
- An electron is in the spin-state
in the Pauli representation. Determine the constant 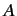 by normalizing
by normalizing
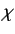 . If a measurement of
. If a measurement of 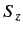 is made, what values will be
obtained, and with what probabilities? What is the expectation
value of
is made, what values will be
obtained, and with what probabilities? What is the expectation
value of 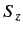 ? Repeat the above calculations for
? Repeat the above calculations for 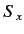 and
and 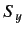 .
.
- Consider a spin-
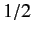 system represented by the normalized spinor
system represented by the normalized spinor
in the Pauli representation, where 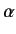 and
and 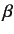 are real. What is the probability that a measurement of
are real. What is the probability that a measurement of
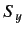 yields
yields 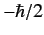 ?
?
- An electron is at rest in an oscillating magnetic field
where 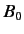 and
and 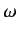 are real positive constants.
are real positive constants.
- Find the Hamiltonian of the system.
- If the electron starts in the spin-up state with respect to the
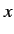 -axis, determine the spinor
-axis, determine the spinor 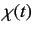 that represents the state
of the system in the Pauli representation at all subsequent times.
that represents the state
of the system in the Pauli representation at all subsequent times.
- Find the probability that a measurement of
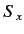 yields
the result
yields
the result 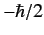 as a function of time.
as a function of time.
- What is the minimum value of
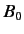 required to force a
complete flip in
required to force a
complete flip in 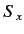 ?
?


Next: Addition of Angular Momentum
Up: Spin Angular Momentum
Previous: Spin Greater Than One-Half
Richard Fitzpatrick
2013-04-08
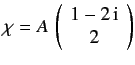
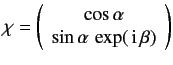
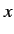 -axis, determine the spinor
-axis, determine the spinor 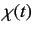 that represents the state
of the system in the Pauli representation at all subsequent times.
that represents the state
of the system in the Pauli representation at all subsequent times.
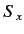 yields
the result
yields
the result 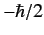 as a function of time.
as a function of time.
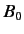 required to force a
complete flip in
required to force a
complete flip in 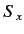 ?
?