

Next: Variational Principle
Up: Identical Particles
Previous: Helium Atom
Orthohelium and Parahelium
Consider an excited state of the helium atom in which one electron is in the ground state, while the other is in a state characterized by the quantum
numbers 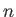 ,
, 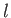 ,
, 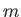 , where
, where 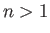 . Making use of the Hamiltonian (9.52), and treating the
final term as a perturbation,
we can write the energy of this state as
. Making use of the Hamiltonian (9.52), and treating the
final term as a perturbation,
we can write the energy of this state as
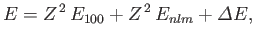 |
(9.64) |
where
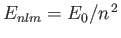 is the energy of a hydrogen atom electron whose quantum numbers are
is the energy of a hydrogen atom electron whose quantum numbers are 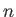 ,
, 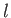 ,
, 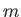 ,
,
 the hydrogen ground-state energy, and
the hydrogen ground-state energy, and
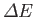 the expectation value of
the expectation value of
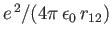 . It follows from Equation (9.53) (with
. It follows from Equation (9.53) (with
 and
and
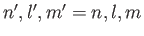 ) that
) that
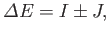 |
(9.65) |
where
and 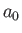 is the Bohr radius.
Here, the plus sign in Equation (9.66) corresponds to the spin-singlet state, whereas the minus sign corresponds to the spin-triplet state. The
integral
is the Bohr radius.
Here, the plus sign in Equation (9.66) corresponds to the spin-singlet state, whereas the minus sign corresponds to the spin-triplet state. The
integral  --which is known as the direct integral--is obviously positive. The integral
--which is known as the direct integral--is obviously positive. The integral 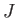 --which is known as the exchange integral--can
be shown also to be positive. (See Exercises 13 and 14.) Hence, we conclude that, in excited states of helium, the spin-singlet state has a higher energy
than the corresponding spin-triplet state. Incidentally, helium in the spin-singlet state is known as parahelium, whereas helium in the triplet state is
called orthohelium. As we have seen, only parahelium is possible in the ground state,
--which is known as the exchange integral--can
be shown also to be positive. (See Exercises 13 and 14.) Hence, we conclude that, in excited states of helium, the spin-singlet state has a higher energy
than the corresponding spin-triplet state. Incidentally, helium in the spin-singlet state is known as parahelium, whereas helium in the triplet state is
called orthohelium. As we have seen, only parahelium is possible in the ground state,
The fact that parahelium energy levels lie slightly above corresponding orthohelium levels is interesting because our original Hamiltonian, (9.52), does not explicitly
depend on spin. Nevertheless, there is a spin dependent effect--that is, a helium atom has a lower energy when its electrons possess parallel spins--as a consequence of
Fermi-Dirac statistics. To be more exact, the energy is lower in the spin-triplet state because the corresponding spatial wavefunction is antisymmetric,
causing the electrons to tend to avoid one another (thereby reducing their electrostatic repulsion).


Next: Variational Principle
Up: Identical Particles
Previous: Helium Atom
Richard Fitzpatrick
2016-01-22