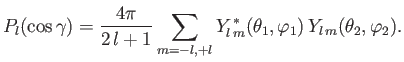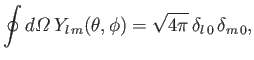Next: Orthohelium and Parahelium
Up: Identical Particles
Previous: Two-Electron System
Helium Atom
Consider the helium atom, which is a good example of a two-electron system. The Hamiltonian is written
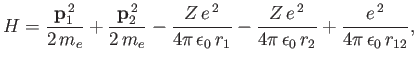 |
(9.51) |
where 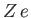 is the nuclear charge,
is the nuclear charge, 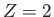 ,
,
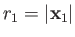 ,
,
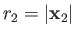 , and
, and
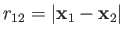 . Here,
. Here, 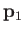 and
and 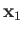 are the momentum and position of the first electron, et cetera.
Suppose that the final term on the right-hand side of the previous expression were absent. In this case, in which the
two electrons do not interact with one another, the overall spatial wavefunction can be formed from products of hydrogen atom wavefunctions calculated with
are the momentum and position of the first electron, et cetera.
Suppose that the final term on the right-hand side of the previous expression were absent. In this case, in which the
two electrons do not interact with one another, the overall spatial wavefunction can be formed from products of hydrogen atom wavefunctions calculated with
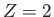 , instead of
, instead of 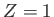 . Each of these wavefunctions is characterized by the usual triplet of quantum numbers,
. Each of these wavefunctions is characterized by the usual triplet of quantum numbers, 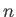 ,
, 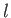 , and
, and 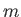 . (See Chapter 4.)
Now, the total spin of the system is a constant of the motion (because
. (See Chapter 4.)
Now, the total spin of the system is a constant of the motion (because 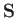 obviously commutes with the Hamiltonian),
so the overall spin state is either the singlet or the triplet state. (See the previous section.) The corresponding spatial wavefunction is symmetric in the former case, and
antisymmetric in the latter. Suppose that one electron has the quantum numbers
obviously commutes with the Hamiltonian),
so the overall spin state is either the singlet or the triplet state. (See the previous section.) The corresponding spatial wavefunction is symmetric in the former case, and
antisymmetric in the latter. Suppose that one electron has the quantum numbers 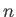 ,
, 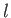 ,
, 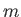 , whereas the other has the quantum numbers
, whereas the other has the quantum numbers 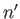 ,
,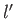 ,
, 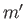 .
The corresponding spatial wavefunction is
.
The corresponding spatial wavefunction is
![$\displaystyle \phi({\bf x}_1,{\bf x}_2)=\frac{1}{\sqrt{2}}\left[\psi_{nlm}({\bf...
..._{n'l'm'}({\bf x}_2)\pm \psi_{nlm}({\bf x}_2)\,\psi_{n'l'm'}({\bf x}_1)\right],$](img3110.png) |
(9.52) |
where the plus and minus signs correspond to the singlet and triplet spin states, respectively. Here,
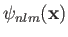 is a standard hydrogen atom wavefunction (calculated with
is a standard hydrogen atom wavefunction (calculated with 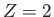 ). For the special case in which the two sets of spatial quantum numbers,
). For the special case in which the two sets of spatial quantum numbers, 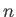 ,
, 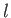 ,
, 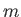 and
and 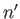 ,
, 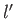 ,
, 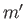 , are the same, the triplet spin state does not exist (because the associated spatial wavefunction is null). Hence, only
singlet spin state is allowed, and the spatial wavefunction reduces to
, are the same, the triplet spin state does not exist (because the associated spatial wavefunction is null). Hence, only
singlet spin state is allowed, and the spatial wavefunction reduces to
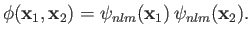 |
(9.53) |
In particular, the ground state (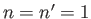 ,
, 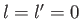 ,
, 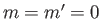 ) can only exist as a singlet spin state (i.e., a state of overall spin 0), and has the
spatial wavefunction
) can only exist as a singlet spin state (i.e., a state of overall spin 0), and has the
spatial wavefunction
![$\displaystyle \phi({\bf x}_1,{\bf x}_2) =\psi_{100}({\bf x}_1)\,\psi_{100}({\bf...
...2)= \frac{Z^{\,3}}{\pi\,a_0^{\,3}}\,\exp\left[\frac{-Z\,(r_1+r_2)}{a_0}\right],$](img3115.png) |
(9.54) |
where 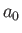 is the Bohr radius. This follows because [see Equation (4.95) and Exercise 8]
is the Bohr radius. This follows because [see Equation (4.95) and Exercise 8]
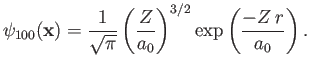 |
(9.55) |
The energy of this state
is
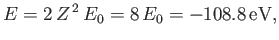 |
(9.56) |
because 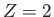 . (See Exercise 8.)
Here,
. (See Exercise 8.)
Here,
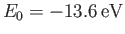 is the ground-state energy of a hydrogen atom. In the previous expression, the factor of
is the ground-state energy of a hydrogen atom. In the previous expression, the factor of 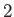 (before the factor
(before the factor 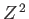 ) is present because
there are two electrons in a helium atom.
) is present because
there are two electrons in a helium atom.
The previous estimate for the ground-state energy of a helium atom completely ignores the final term on the right-hand side of Equation (9.52),
which describes the mutual electrostatic repulsion of the two electrons. We can obtain a better estimate for the ground-state energy by treating Equation (9.55)
as the unperturbed wavefunction, and
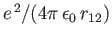 as a perturbation. According to standard first-order perturbation theory (see Chapter 7), the
correction to the ground-state energy is
as a perturbation. According to standard first-order perturbation theory (see Chapter 7), the
correction to the ground-state energy is
because
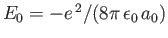 . Here, the expectation value is calculated using the wavefunction (9.55).
The resulting expression for
. Here, the expectation value is calculated using the wavefunction (9.55).
The resulting expression for
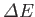 can be written
can be written
![$\displaystyle \frac{{\mit\Delta E}}{\vert E_0\vert} = \frac{2\,Z^{\,6}}{\pi^{\,...
...}{a_0^{\,3}}\,\exp\left[-\frac{2\,Z\,(r_1+r_2)}{a_0}\right] \frac{a_0}{r_{12}}.$](img3124.png) |
(9.58) |
Now,
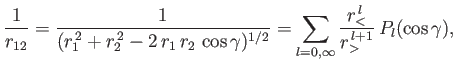 |
(9.59) |
where 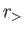 (
(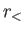 ) is the larger (smaller) of
) is the larger (smaller) of 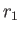 and
and 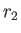 ,
, 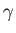 the angle subtended between
the angle subtended between 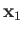 and
and 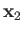 , and
, and 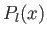 a Legendre polynomial [50].
Moreover, the so-called addition theorem for spherical harmonics states that [67]
a Legendre polynomial [50].
Moreover, the so-called addition theorem for spherical harmonics states that [67]
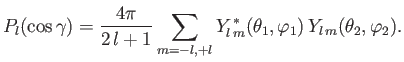 |
(9.60) |
Here,
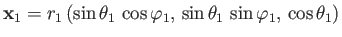 , et cetera.
However [see Equations (4.94) and (4.95)],
, et cetera.
However [see Equations (4.94) and (4.95)],
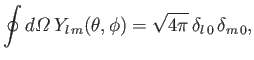 |
(9.61) |
so, combining the previous four equations, we obtain
(See Exercise 10.)
Here,
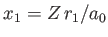 and
and
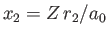 .
Thus, our improved estimate for the ground-state energy of the helium atom is [113]
.
Thus, our improved estimate for the ground-state energy of the helium atom is [113]
because 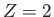 and
and
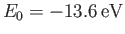 .
This is much closer to the experimental value of
.
This is much closer to the experimental value of
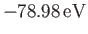 [75] than our previous estimate,
[75] than our previous estimate,
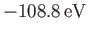 . [See Equation (9.57).]
. [See Equation (9.57).]



Next: Orthohelium and Parahelium
Up: Identical Particles
Previous: Two-Electron System
Richard Fitzpatrick
2016-01-22
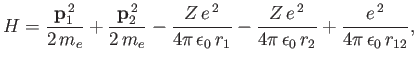
![]() as a perturbation. According to standard first-order perturbation theory (see Chapter 7), the
correction to the ground-state energy is
as a perturbation. According to standard first-order perturbation theory (see Chapter 7), the
correction to the ground-state energy is
![$\displaystyle \frac{{\mit\Delta E}}{\vert E_0\vert} = \frac{2\,Z^{\,6}}{\pi^{\,...
...}{a_0^{\,3}}\,\exp\left[-\frac{2\,Z\,(r_1+r_2)}{a_0}\right] \frac{a_0}{r_{12}}.$](img3124.png)