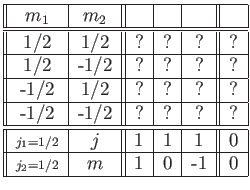
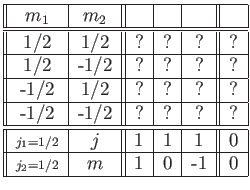
The box in this table corresponding to
A Clebsch-Gordon coefficient is automatically zero unless
![]() . In other words, the
. In other words, the ![]() -components of angular momentum have to
add algebraically. Many of the boxes in the previous table correspond to
-components of angular momentum have to
add algebraically. Many of the boxes in the previous table correspond to
![]() . We immediately conclude that these boxes must contain zeroes.
Thus,
. We immediately conclude that these boxes must contain zeroes.
Thus,
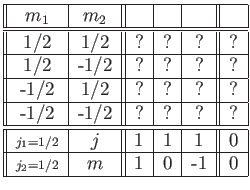
The normalization condition (6.28) implies that the sum of the squares
of all the rows and columns of the previous table must be unity. There are two
rows and two columns that contain only a single non-zero entry. We conclude that
these entries must be ![]() , but we have no way of determining the
signs at present. Thus,
, but we have no way of determining the
signs at present. Thus,
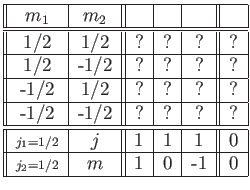
Let us evaluate the recursion relation (6.32) for
![]() , with
, with
![]() ,
, ![]() ,
,
![]() , taking the upper/lower sign. We
find that
, taking the upper/lower sign. We
find that
| (6.32) |
| (6.33) |
| (6.34) |
| (6.35) |
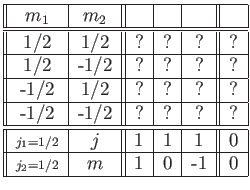
We could fill in the remaining unknown entries of our table by using the recursion
relation again. However, an easier method is to observe that the rows and columns
of the table must all be mutually orthogonal. That is, the dot product
of a row with any other row must be zero. Likewise, for the dot product of
a column with any other column. This follows because the entries in the
table give the expansion coefficients of one of our alternative sets of eigenkets
in terms of the other set, and each set of eigenkets contains
mutually orthogonal vectors with unit norms. The normalization
condition tells us that the dot product of a row or column with itself must
be unity. The only way that the dot product of the fourth column with
the second column can be zero is if the unknown entries are equal and opposite.
The requirement that the dot product of the fourth column with itself is
unity tells us that the magnitudes of the unknown entries have to be
![]() .
The unknown entries are undetermined to an arbitrary sign multiplied into them both.
Thus, the final form of our table (with the conventional choice of arbitrary
signs) is
.
The unknown entries are undetermined to an arbitrary sign multiplied into them both.
Thus, the final form of our table (with the conventional choice of arbitrary
signs) is
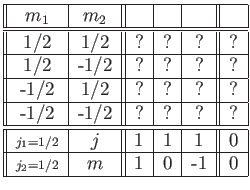
The table can be read in one of two ways. The columns give the expansions of the eigenstates of overall angular momentum in terms of the eigenstates of the individual angular momenta of the two component systems. Thus, the second column tells us that
 |
(6.36) |
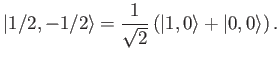 |
(6.37) |
Note that our table is really a combination of two sub-tables, one involving
![]() states, and one involving
states, and one involving ![]() states. The Clebsch-Gordon coefficients
corresponding to two different choices of
states. The Clebsch-Gordon coefficients
corresponding to two different choices of ![]() are completely independent.
That is, there is no recursion relation linking Clebsch-Gordon coefficients
corresponding to different values of
are completely independent.
That is, there is no recursion relation linking Clebsch-Gordon coefficients
corresponding to different values of ![]() . Thus, for every choice of
. Thus, for every choice of ![]() ,
, ![]() ,
and
,
and ![]() we can construct a table of Clebsch-Gordon coefficients corresponding
to the different allowed values of
we can construct a table of Clebsch-Gordon coefficients corresponding
to the different allowed values of ![]() ,
, ![]() , and
, and ![]() (subject to the
constraint that
(subject to the
constraint that ![]() ). A complete knowledge of angular momentum addition
is equivalent to knowing all possible tables of Clebsch-Gordon coefficients.
These tables are listed (for moderate values of
). A complete knowledge of angular momentum addition
is equivalent to knowing all possible tables of Clebsch-Gordon coefficients.
These tables are listed (for moderate values of
![]() and
and ![]() ) in many standard reference books and articles [7].
) in many standard reference books and articles [7].