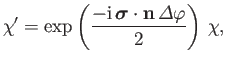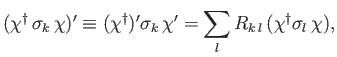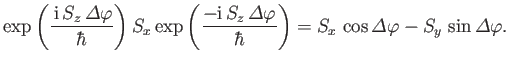

Next: Factorization of Spinor-Wavefunctions
Up: Spin Angular Momentum
Previous: Pauli Two-Component Formalism
Spinor Rotation Matrices
A general rotation operator in spin space is written
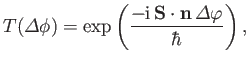 |
(5.95) |
by analogy with Equation (5.24), where 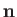 is a unit vector pointing along
the axis of rotation, and
is a unit vector pointing along
the axis of rotation, and
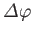 is the angle of rotation.
Here,
is the angle of rotation.
Here, 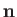 can be regarded as a trivial position operator. The
rotation operator is represented
can be regarded as a trivial position operator. The
rotation operator is represented
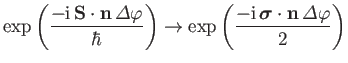 |
(5.96) |
in the Pauli scheme.
The term on the right-hand side of the previous expression is the exponential
of a matrix. This can easily be evaluated using the Taylor series for an exponential,
plus the rules
These rules follow trivially from the identity (5.93). Thus, we can write
The explicit 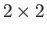 form of this matrix is
form of this matrix is
 |
(5.100) |
Rotation matrices act on spinors in much the same manner as the corresponding
rotation operators act on state kets. Thus,
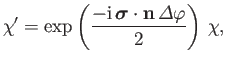 |
(5.101) |
where 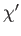 denotes the spinor obtained after rotating the spinor
denotes the spinor obtained after rotating the spinor
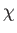 an angle
an angle
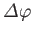 about the axis
about the axis 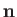 .
The Pauli matrices remain unchanged under rotations.
However, the quantity
.
The Pauli matrices remain unchanged under rotations.
However, the quantity
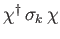 is proportional to the expectation
value of
is proportional to the expectation
value of 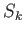 [see Equation (5.75)], so we would expect it to transform like a
vector under rotation. (See Section 5.4.) In fact, we
require
[see Equation (5.75)], so we would expect it to transform like a
vector under rotation. (See Section 5.4.) In fact, we
require
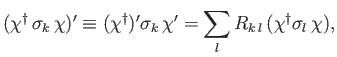 |
(5.102) |
where the 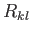 are the elements of a conventional rotation matrix [92]. This
is easily demonstrated, because
are the elements of a conventional rotation matrix [92]. This
is easily demonstrated, because
 |
(5.103) |
plus all cyclic permutations. The previous expression is the  matrix analog
of
matrix analog
of
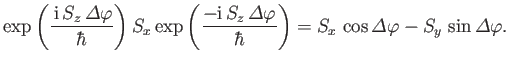 |
(5.104) |
[See Equation (5.30).]
Equation (5.103) follows from the Baker-Campbell-Hausdorff lemma,
(5.31), which holds for matrices, in addition to operators.


Next: Factorization of Spinor-Wavefunctions
Up: Spin Angular Momentum
Previous: Pauli Two-Component Formalism
Richard Fitzpatrick
2016-01-22
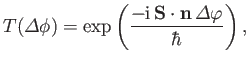
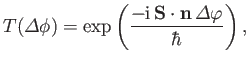
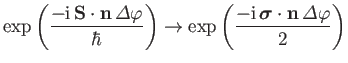
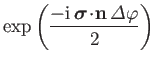
![$\displaystyle = \left[ 1 - \frac{(\mbox{\boldmath$\sigma$}\cdot {\bf n})^2}{2!}...
...t {\bf n})^4}{4!} \left(\frac{{\mit\Delta}\varphi}{2} \right)^4 + \cdots\right]$](img1503.png)
![$\displaystyle \phantom{=}- {\rm i} \left[ (\mbox{\boldmath$\sigma$}\cdot {\bf n...
...ot {\bf n})^3}{3!} \left(\frac{{\mit\Delta}\varphi}{2}\right)^3 + \cdots\right]$](img1504.png)