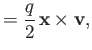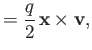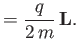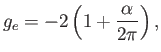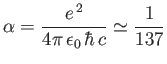

Next: Spin Precession
Up: Spin Angular Momentum
Previous: Rotation Operators in Spin
Magnetic Moments
Consider a particle of electric charge  and speed
and speed 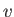 performing a circular orbit of radius
performing a circular orbit of radius 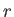 in the
in the 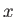 -
-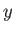 plane. The charge is equivalent to a current loop of radius
plane. The charge is equivalent to a current loop of radius 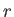 , lying
in the
, lying
in the 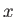 -
-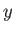 plane, and carrying a current
plane, and carrying a current
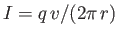 . The magnetic moment
. The magnetic moment
 of
the loop is of magnitude
of
the loop is of magnitude
 and is directed along the
and is directed along the 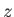 -axis (the direction is given
by a right-hand rule with the fingers of the right-hand circulating in the same direction as the current) [49].
Thus, we can write
-axis (the direction is given
by a right-hand rule with the fingers of the right-hand circulating in the same direction as the current) [49].
Thus, we can write
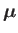 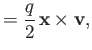 |
(5.42) |
where  and
and 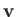 are the vector position and velocity of the particle,
respectively. However, we know that
are the vector position and velocity of the particle,
respectively. However, we know that
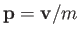 , where
, where 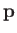 is the particle's vector momentum, and
is the particle's vector momentum, and 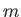 its mass. We also know that
its mass. We also know that
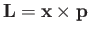 , where
, where 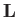 is the orbital angular momentum.
It follows that
is the orbital angular momentum.
It follows that
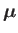 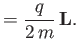 |
(5.43) |
Using the standard analogy between classical and quantum mechanics, we
expect the previous relation to also hold between the quantum mechanical operators,
 and
and 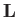 , which represent magnetic moment and orbital angular momentum,
respectively.
This is indeed found to the the case experimentally.
, which represent magnetic moment and orbital angular momentum,
respectively.
This is indeed found to the the case experimentally.
Spin angular momentum also gives rise to a contribution to the magnetic
moment of a charged particle. In fact, relativistic quantum
mechanics predicts that a charged particle possessing spin must also
possess a corresponding magnetic moment [30,32,9]. We can write
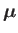 ![$\displaystyle = \frac{q}{2\,m} \left[{\bf L} + {\rm sgn}(q)\,g \,{\bf S}\right],$](img1388.png) |
(5.44) |
where the parameter 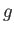 is called the
is called the 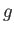 -factor. For an electron this factor
is found to be
-factor. For an electron this factor
is found to be
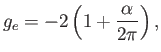 |
(5.45) |
where
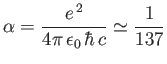 |
(5.46) |
is the fine structure constant.
The factor 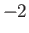 is correctly predicted by Dirac's famous relativistic theory of the electron [30,32]. (See Chapter 11.)
The small correction
is correctly predicted by Dirac's famous relativistic theory of the electron [30,32]. (See Chapter 11.)
The small correction
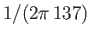 is due to
quantum field effects [101]. We shall ignore this correction in the following,
so
is due to
quantum field effects [101]. We shall ignore this correction in the following,
so
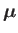 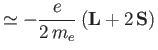 |
(5.47) |
for an electron. (Here,  is the magnitude of the electron charge, and
is the magnitude of the electron charge, and 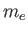 the electron mass.)
the electron mass.)


Next: Spin Precession
Up: Spin Angular Momentum
Previous: Rotation Operators in Spin
Richard Fitzpatrick
2016-01-22