


Next: Motion in Central Field
Up: Orbital Angular Momentum
Previous: Rotation Operators
Eigenfunctions of Orbital Angular Momentum
In Cartesian coordinates, the three components of orbital angular
momentum can be written
using the Schrödinger representation. Transforming to standard
spherical coordinates,
we obtain
(See Exercise 2.)
Note that Equation (4.82) accords with Equation (4.57). The ladder
operators
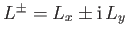 become
become
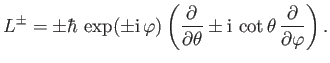 |
(4.83) |
(See Exercise 2.) Now,
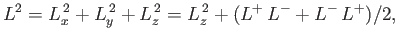 |
(4.84) |
so
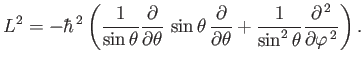 |
(4.85) |
(See Exercise 2.)
The eigenvalue problem for
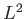 takes the form
takes the form
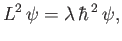 |
(4.86) |
where
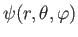 is the wavefunction, and
is the wavefunction, and 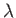 is a dimensionless number.
Let us write
is a dimensionless number.
Let us write
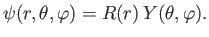 |
(4.87) |
Equation (4.86) reduces to
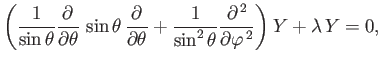 |
(4.88) |
where use has been made of Equation (4.85). As is well known,
square-integrable solutions to this
equation only exist when 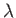 takes the values
takes the values 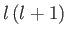 , where
, where 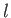 is
an integer (which we can take to be non-negative, without loss of generality) [76]. These solutions are known as spherical harmonics [67], and
can be written
is
an integer (which we can take to be non-negative, without loss of generality) [76]. These solutions are known as spherical harmonics [67], and
can be written
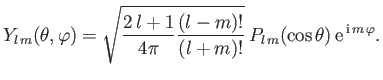 |
(4.89) |
Here,
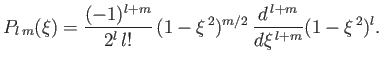 |
(4.90) |
is an associated Legendre function [67], satisfying the
equation
![$\displaystyle \frac{d}{d\xi}\! \left[ (1-\xi^{\,2})\,\frac{dP_{l\,m}}{d\xi}\right] - \frac{m^{\,2}}{1-\xi^{\,2}}\, P_{l\,m} + l\,(l+1)\,P_{l\,m} = 0.$](img1110.png) |
(4.91) |
It follows that
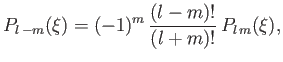 |
(4.92) |
and, hence, that
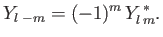 |
(4.93) |
Of course, 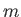 must be an integer, so as to ensure that the
must be an integer, so as to ensure that the 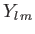 are single valued in
are single valued in 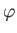 . Moreover, it is clear from
Equations (4.90) and (4.92) that
. Moreover, it is clear from
Equations (4.90) and (4.92) that
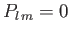 unless
unless
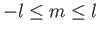 .
The spherical harmonics are orthogonal functions, and are
properly normalized with respect to integration over
the entire solid angle [67]:
.
The spherical harmonics are orthogonal functions, and are
properly normalized with respect to integration over
the entire solid angle [67]:
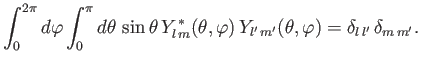 |
(4.94) |
The spherical harmonics also form a complete set for representing general functions
of 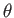 and
and 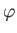 .
The first few spherical harmonics are [67]:
.
The first few spherical harmonics are [67]:
By definition,
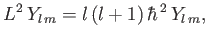 |
(4.105) |
where 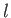 is an integer.
It follows from Equations (4.82) and (4.89) that
is an integer.
It follows from Equations (4.82) and (4.89) that
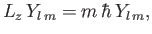 |
(4.106) |
where 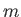 is an integer lying in the range
is an integer lying in the range
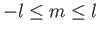 . Thus, the
wavefunction
. Thus, the
wavefunction
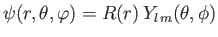 , where
, where
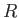 is a general function, has
all of the expected features of the wavefunction
of a simultaneous eigenstate of
is a general function, has
all of the expected features of the wavefunction
of a simultaneous eigenstate of 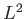 and
and 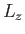 belonging to the quantum numbers
belonging to the quantum numbers 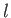 and
and 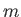 . The well-known formula [1]
. The well-known formula [1]
can be combined with Equations (4.83) and (4.89) to give
(See Exercise 4.)
These equations are equivalent to Equations (4.55)-(4.56). Note that a spherical
harmonic wavefunction
is symmetric about the 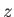 -axis (i.e., independent of
-axis (i.e., independent of 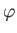 ) whenever
) whenever
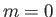 , and is spherically symmetric whenever
, and is spherically symmetric whenever 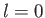 (because
(because
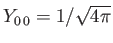 ).
).
In summary, by solving directly
for the
eigenfunctions of 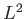 and
and 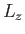 in the Schrödinger representation, we have been able to reproduce
all of the results of Section 4.2. Nevertheless, the results of Section 4.2
are more general than those obtained in this section, because they still apply
when the quantum number
in the Schrödinger representation, we have been able to reproduce
all of the results of Section 4.2. Nevertheless, the results of Section 4.2
are more general than those obtained in this section, because they still apply
when the quantum number 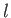 takes on half-integer values.
takes on half-integer values.



Next: Motion in Central Field
Up: Orbital Angular Momentum
Previous: Rotation Operators
Richard Fitzpatrick
2016-01-22
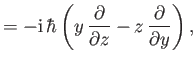
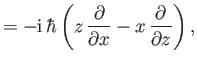
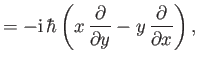
![]() takes the form
takes the form
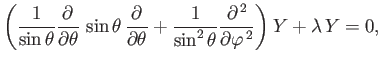
![$\displaystyle \frac{d}{d\xi}\! \left[ (1-\xi^{\,2})\,\frac{dP_{l\,m}}{d\xi}\right] - \frac{m^{\,2}}{1-\xi^{\,2}}\, P_{l\,m} + l\,(l+1)\,P_{l\,m} = 0.$](img1110.png)
![]() and
and ![]() in the Schrödinger representation, we have been able to reproduce
all of the results of Section 4.2. Nevertheless, the results of Section 4.2
are more general than those obtained in this section, because they still apply
when the quantum number
in the Schrödinger representation, we have been able to reproduce
all of the results of Section 4.2. Nevertheless, the results of Section 4.2
are more general than those obtained in this section, because they still apply
when the quantum number ![]() takes on half-integer values.
takes on half-integer values.