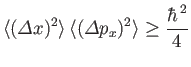

Next: Displacement Operators
Up: Position and Momentum
Previous: Momentum Representation
Heisenberg Uncertainty Principle
How is a momentum space wavefunction related to the corresponding coordinate
space wavefunction? To answer this question, let us consider the
representative
 of the
momentum eigenkets
of the
momentum eigenkets
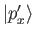 in the Schrödinger representation
for a system with a single degree of freedom. This representative satisfies
in the Schrödinger representation
for a system with a single degree of freedom. This representative satisfies
 |
(2.91) |
where use has been made of Equation (2.78) (for the case of a system with one
degree of freedom). The solution of the previous differential equation is
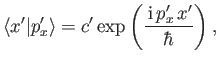 |
(2.92) |
where
 . It is easily demonstrated that
. It is easily demonstrated that
The well-known mathematical result [92]
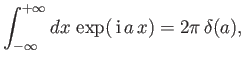 |
(2.94) |
yields
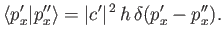 |
(2.95) |
This is consistent with Equation (2.80), provided that
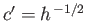 . Thus,
. Thus,
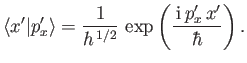 |
(2.96) |
Consider a general state ket 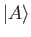 whose coordinate wavefunction is
whose coordinate wavefunction is 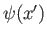 ,
and whose momentum wavefunction is
,
and whose momentum wavefunction is
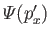 . In other words,
. In other words,
It is easily demonstrated that
 |
(2.99) |
and
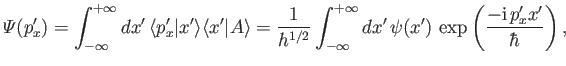 |
(2.100) |
where use has been made of Equations (2.27), (2.81), (2.94), and (2.96).
Clearly, the momentum
space wavefunction is the Fourier transform
of the corresponding coordinate space wavefunction [51].
Consider a state whose coordinate space wavefunction is a wavepacket.
In other words, the wavefunction only has non-negligible amplitude in some
spatially localized region of extent
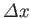 . As is well known, the Fourier
transform of a wavepacket fills up a wavenumber band of approximate extent
. As is well known, the Fourier
transform of a wavepacket fills up a wavenumber band of approximate extent
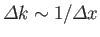 . [51]. Note that, in Equation (2.99), the role of the wavenumber
. [51]. Note that, in Equation (2.99), the role of the wavenumber
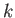 is played by the quantity
is played by the quantity
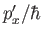 . It follows that the momentum space
wavefunction corresponding to a wavepacket in coordinate space extends over
a range of momenta
. It follows that the momentum space
wavefunction corresponding to a wavepacket in coordinate space extends over
a range of momenta
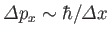 . Clearly, a measurement
of
. Clearly, a measurement
of 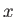 is almost certain to give a result lying in a
range of width
is almost certain to give a result lying in a
range of width
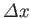 . Likewise, measurement of
. Likewise, measurement of 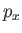 is almost certain to
yield a result lying in a range of width
is almost certain to
yield a result lying in a range of width
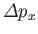 . The product of these two
uncertainties is
. The product of these two
uncertainties is
 |
(2.101) |
This result is called the Heisenberg uncertainty principle [65].
Actually, it is possible to write the Heisenberg uncertainty principle
more exactly by making use of
Equation (1.86) and the commutation relation (2.47). We obtain
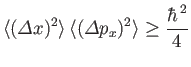 |
(2.102) |
for a general state. It is easily demonstrated that the minimum uncertainty states,
for which the equality sign holds in the previous relation, correspond to Gaussian
wavepackets in both coordinate and momentum space. (See Exercise 4.)


Next: Displacement Operators
Up: Position and Momentum
Previous: Momentum Representation
Richard Fitzpatrick
2016-01-22


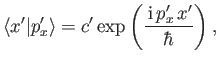
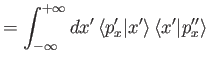
![$\displaystyle = c'^{\,\ast}\, c'' \int_{-\infty}^{\infty}dx'\,\exp\left[\frac{-{\rm i}\, (p_x'-p_x'')\,x'}{\hbar}\right].$](img471.png)
![]() whose coordinate wavefunction is
whose coordinate wavefunction is ![]() ,
and whose momentum wavefunction is
,
and whose momentum wavefunction is
![]() . In other words,
. In other words,
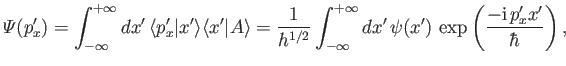
![]() . As is well known, the Fourier
transform of a wavepacket fills up a wavenumber band of approximate extent
. As is well known, the Fourier
transform of a wavepacket fills up a wavenumber band of approximate extent
![]() . [51]. Note that, in Equation (2.99), the role of the wavenumber
. [51]. Note that, in Equation (2.99), the role of the wavenumber
![]() is played by the quantity
is played by the quantity
![]() . It follows that the momentum space
wavefunction corresponding to a wavepacket in coordinate space extends over
a range of momenta
. It follows that the momentum space
wavefunction corresponding to a wavepacket in coordinate space extends over
a range of momenta
![]() . Clearly, a measurement
of
. Clearly, a measurement
of ![]() is almost certain to give a result lying in a
range of width
is almost certain to give a result lying in a
range of width
![]() . Likewise, measurement of
. Likewise, measurement of ![]() is almost certain to
yield a result lying in a range of width
is almost certain to
yield a result lying in a range of width
![]() . The product of these two
uncertainties is
. The product of these two
uncertainties is