


Next: Physical Constants
Up: Relativistic Electron Theory
Previous: Positron Theory
- Demonstrate that the four operators
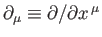 transform under Lorentz transformation
as the covariant components of 4-vector, whereas the four operators
transform under Lorentz transformation
as the covariant components of 4-vector, whereas the four operators
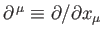 transform
as the contravariant components of the same vector.
transform
as the contravariant components of the same vector.
- Demonstrate that Equation (11.29) is equivalent to Equations (11.24)-(11.26).
- Noting that
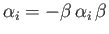 , prove that the
, prove that the 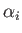 and
and 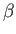 matrices all have zero trace. Hence,
deduce that each of these matrices has
matrices all have zero trace. Hence,
deduce that each of these matrices has 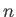 eigenvalues
eigenvalues 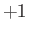 , and
, and 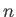 eigenvalues
eigenvalues 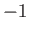 , where
, where 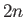 is the dimension
of the matrices.
is the dimension
of the matrices.
- Verify that the matrices (11.30) and (11.31) satisfy the anti-commutation relations (11.29).
- Verify that the matrices (11.32) and (11.33) satisfy Equations (11.24)-(11.26).
- Verify that if
where 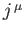 is a 4-vector field, then
is a 4-vector field, then
is Lorentz invariant, where the integral is over all space, and it is assumed that
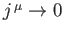 as
as
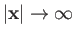 .
.
- Verify that Equation (11.77) is a solution of Equations (11.76).
- A Lorentz transformation between frames
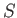 and
and 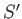 takes the form
takes the form
If
where
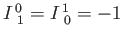 , and
, and
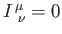 otherwise, then the transformation corresponds to an infinitesimal
velocity boost,
otherwise, then the transformation corresponds to an infinitesimal
velocity boost,
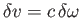 , parallel to the
, parallel to the 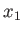 -axis. Show that if a finite boost is built up from a great many
such boosts then the transformation matrix becomes
-axis. Show that if a finite boost is built up from a great many
such boosts then the transformation matrix becomes
where
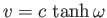 is the velocity of frame
is the velocity of frame 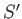 relative to frame
relative to frame 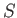 . Show that the corresponding transformation rule for spinor wavefunctions is
. Show that the corresponding transformation rule for spinor wavefunctions is
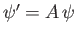 , where
, where
- Show that the transformation rule for spinor wavefunctions associated with a Lorentz transformation from frame
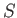 to some frame
to some frame 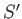 moving with velocity
moving with velocity
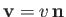 with respect to
with respect to 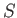 is
is
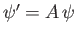 , where
, where
and
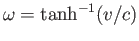 .
.
- Consider the spinors
for 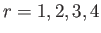 . Here,
. Here,
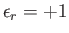 for
for 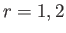 , and
, and
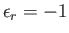 for
for 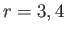 . Moreover,
. Moreover,
Verify that the
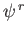 are solutions of the Dirac equation in free space corresponding to electrons of
energy
are solutions of the Dirac equation in free space corresponding to electrons of
energy
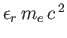 , momentum
, momentum
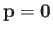 , and spin angular momentum parallel to the
, and spin angular momentum parallel to the 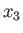 -axis
-axis
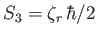 , where
, where
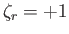 for
for 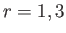 , and
, and
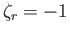 for
for 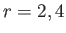 .
.
- Show that the four solutions of the Dirac equation corresponding to an electron
of energy
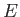 and momentum
and momentum 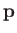 moving in free space take the form
moving in free space take the form
where
Here,
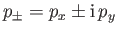 . Demonstrate that these spinors become identical to the
. Demonstrate that these spinors become identical to the
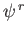 of the previous exercise in the limit that
of the previous exercise in the limit that
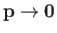 .
.
- Verify that the
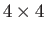 matrices
matrices
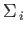 , defined in Equation (11.98), satisfy the standard anti-commutation
relations for Pauli matrices: that is,
, defined in Equation (11.98), satisfy the standard anti-commutation
relations for Pauli matrices: that is,



Next: Physical Constants
Up: Relativistic Electron Theory
Previous: Positron Theory
Richard Fitzpatrick
2016-01-22
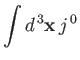
![\begin{displaymath}
a^{\,\mu}_{~\nu}=\left(
\begin{array}{cccc}\cosh\omega, &-\s...
...\\ [0.5ex]
0,&0,&1,&0\\ [0.5ex]
0,&0,&0,&1
\end{array}\right),
\end{displaymath}](img4206.png)
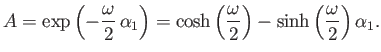
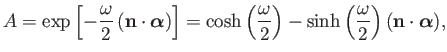
![$\displaystyle =\left(\begin{array}{c}1\\ [0.5ex]0\\ [0.5ex]0\\ [0.5ex]0\end{array}\right),$](img4220.png)
![$\displaystyle =\left(\begin{array}{c}0\\ [0.5ex]1\\ [0.5ex]0\\ [0.5ex]0\end{array}\right),$](img4222.png)
![$\displaystyle =\left(\begin{array}{c}0\\ [0.5ex]0\\ [0.5ex]1\\ [0.5ex]0\end{array}\right),$](img4224.png)
![$\displaystyle =\left(\begin{array}{c}0\\ [0.5ex]0\\ [0.5ex]0\\ [0.5ex]1\end{array}\right).$](img4226.png)
![$\displaystyle =\sqrt{\frac{E+m_e\,c^{\,2}}{2\,m_e\,c^{\,2}}}\left(\begin{array}...
...z\,c}{E+m_e\,c^{\,2}}\\ [0.5ex]\frac{p_+\,c}{E+m_e\,c^{\,2}}\end{array}\right),$](img4238.png)
![$\displaystyle =\sqrt{\frac{E+m_e\,c^{\,2}}{2\,m_e\,c^{\,2}}}\left(\begin{array}...
...\,c}{E+m_e\,c^{\,2}}\\ [0.5ex]\frac{-p_z\,c}{E+m_e\,c^{\,2}}\end{array}\right),$](img4240.png)
![$\displaystyle =\sqrt{\frac{E+m_e\,c^{\,2}}{2\,m_e\,c^{\,2}}}\left(\begin{array}...
... [0.5ex]\frac{p_+\,c}{E+m_e\,c^{\,2}}\\ [0.5ex]1\\ [0.5ex] 0\end{array}\right),$](img4242.png)
![$\displaystyle =\sqrt{\frac{E+m_e\,c^{\,2}}{2\,m_e\,c^{\,2}}}\left(\begin{array}...
...[0.5ex]\frac{-p_z\,c}{E+m_e\,c^{\,2}}\\ [0.5ex]0\\ [0.5ex] 1\end{array}\right).$](img4244.png)
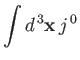
![\begin{displaymath}
a^{\,\mu}_{~\nu}=\left(
\begin{array}{cccc}\cosh\omega, &-\s...
...\\ [0.5ex]
0,&0,&1,&0\\ [0.5ex]
0,&0,&0,&1
\end{array}\right),
\end{displaymath}](img4206.png)
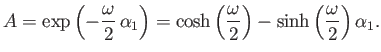
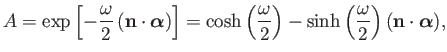
![$\displaystyle =\left(\begin{array}{c}1\\ [0.5ex]0\\ [0.5ex]0\\ [0.5ex]0\end{array}\right),$](img4220.png)
![$\displaystyle =\left(\begin{array}{c}0\\ [0.5ex]1\\ [0.5ex]0\\ [0.5ex]0\end{array}\right),$](img4222.png)
![$\displaystyle =\left(\begin{array}{c}0\\ [0.5ex]0\\ [0.5ex]1\\ [0.5ex]0\end{array}\right),$](img4224.png)
![$\displaystyle =\left(\begin{array}{c}0\\ [0.5ex]0\\ [0.5ex]0\\ [0.5ex]1\end{array}\right).$](img4226.png)
![$\displaystyle =\sqrt{\frac{E+m_e\,c^{\,2}}{2\,m_e\,c^{\,2}}}\left(\begin{array}...
...z\,c}{E+m_e\,c^{\,2}}\\ [0.5ex]\frac{p_+\,c}{E+m_e\,c^{\,2}}\end{array}\right),$](img4238.png)
![$\displaystyle =\sqrt{\frac{E+m_e\,c^{\,2}}{2\,m_e\,c^{\,2}}}\left(\begin{array}...
...\,c}{E+m_e\,c^{\,2}}\\ [0.5ex]\frac{-p_z\,c}{E+m_e\,c^{\,2}}\end{array}\right),$](img4240.png)
![$\displaystyle =\sqrt{\frac{E+m_e\,c^{\,2}}{2\,m_e\,c^{\,2}}}\left(\begin{array}...
... [0.5ex]\frac{p_+\,c}{E+m_e\,c^{\,2}}\\ [0.5ex]1\\ [0.5ex] 0\end{array}\right),$](img4242.png)
![$\displaystyle =\sqrt{\frac{E+m_e\,c^{\,2}}{2\,m_e\,c^{\,2}}}\left(\begin{array}...
...[0.5ex]\frac{-p_z\,c}{E+m_e\,c^{\,2}}\\ [0.5ex]0\\ [0.5ex] 1\end{array}\right).$](img4244.png)