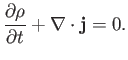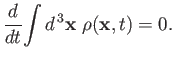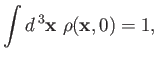Next: Lorentz Invariance of Dirac
Up: Relativistic Electron Theory
Previous: Preliminary Analysis
Consider the motion of an electron in the absence of electromagnetic fields. In classical relativity,
electron energy, 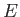 , is related to electron momentum,
, is related to electron momentum, 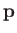 , according to the well-known formula
, according to the well-known formula
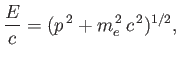 |
(11.15) |
where  is the electron rest mass [93].
The quantum mechanical equivalent of this expression is the wave equation
is the electron rest mass [93].
The quantum mechanical equivalent of this expression is the wave equation
![$\displaystyle \left[p^{\,0} - (p^{\,1}\,p^{\,1}+p^{\,2}\,p^{\,2}+p^{\,3}\,p^{\,3}+m_e^{\,2}\,c^{\,2})^{1/2}\right]\psi = 0,$](img3838.png) |
(11.16) |
where the  's are interpreted as differential operators according to Equation (11.14). The previous equation
takes into account the correct relativistic relation between electron energy and momentum, but is nevertheless unsatisfactory from the
point of view of relativistic theory, because it is highly asymmetric between
's are interpreted as differential operators according to Equation (11.14). The previous equation
takes into account the correct relativistic relation between electron energy and momentum, but is nevertheless unsatisfactory from the
point of view of relativistic theory, because it is highly asymmetric between 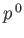 and the other
and the other 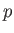 's. This makes the equation
difficult to generalize, in a manifestly Lorentz-invariant manner, in the presence of electromagnetic fields. We must therefore look for a new equation.
's. This makes the equation
difficult to generalize, in a manifestly Lorentz-invariant manner, in the presence of electromagnetic fields. We must therefore look for a new equation.
If we multiply the wave equation (11.16) by the operator
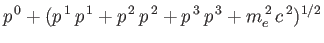 |
(11.17) |
then we obtain
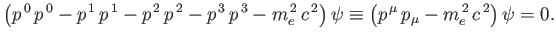 |
(11.18) |
This equation is manifestly Lorentz invariant, and, therefore, forms a more convenient starting point for relativistic quantum mechanics.
Note, however, that Equation (11.18) is not entirely equivalent to Equation (11.16), because, although each
solution of Equation (11.16) is also a solution of Equation (11.18), the converse is not true. In fact, only those solutions of Equation (11.18)
belonging to positive values of 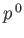 are also solutions of Equation (11.16).
are also solutions of Equation (11.16).
The wave equation (11.18) is quadratic in 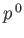 , and is, thus, not of the form required by the laws of quantum theory. (Recall that we demonstrated, from
general principles, in Chapter 3, that the
time evolution equation for the wavefunction should be linear in the operator
, and is, thus, not of the form required by the laws of quantum theory. (Recall that we demonstrated, from
general principles, in Chapter 3, that the
time evolution equation for the wavefunction should be linear in the operator
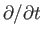 , and, hence, in
, and, hence, in 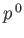 .) We, therefore, seek a wave equation that is
equivalent to Equation (11.18), but is
linear in
.) We, therefore, seek a wave equation that is
equivalent to Equation (11.18), but is
linear in 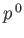 . In order to ensure that this equation transforms in a simple way under a Lorentz transformation, we
shall require it to be rational and linear in
. In order to ensure that this equation transforms in a simple way under a Lorentz transformation, we
shall require it to be rational and linear in 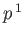 ,
, 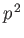 ,
, 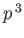 , as well as
, as well as 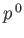 . We are, thus,
lead to a wave equation of the form
. We are, thus,
lead to a wave equation of the form
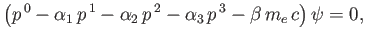 |
(11.19) |
where the 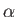 's and
's and 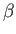 are dimensionless, and independent of the
are dimensionless, and independent of the 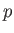 's. Moreover, according to standard relativity, because we are considering the case of no electromagnetic fields, all points in space-time
must be equivalent. Hence, the
's. Moreover, according to standard relativity, because we are considering the case of no electromagnetic fields, all points in space-time
must be equivalent. Hence, the 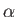 's and
's and 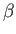 must also be independent of
the
must also be independent of
the 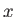 's. This implies that the
's. This implies that the 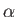 's and
's and 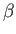 commute with the
commute with the 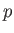 's and the
's and the 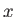 's. We, therefore, deduce that the
's. We, therefore, deduce that the 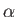 's and
's and 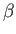 describe an internal degree of freedom that is independent of space-time coordinates. In fact, we shall demonstrate later on in this chapter that these operators are related to electron spin. Note that the previous equation can be
written in the standard form
describe an internal degree of freedom that is independent of space-time coordinates. In fact, we shall demonstrate later on in this chapter that these operators are related to electron spin. Note that the previous equation can be
written in the standard form
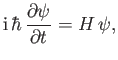 |
(11.20) |
where the effective Hamiltonian, 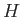 , is
, is
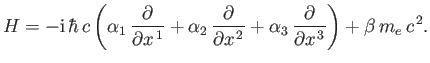 |
(11.21) |
Multiplying Equation (11.19) by the operator
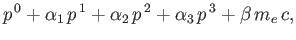 |
(11.22) |
we obtain
![$\displaystyle \left[p^{\,0}\,p^{\,0}-\frac{1}{2}\sum_{i,j=1,3}\{\alpha_i,\alpha...
...a_{\,i},\beta\}\,p^{\,i}\,m_e\,c-\beta^{\,2}\,m_e^{\,2}\,c^{\,2}\right]\psi= 0,$](img3847.png) |
(11.23) |
where
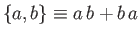 .
This equation is equivalent to Equation (11.18) provided that
.
This equation is equivalent to Equation (11.18) provided that
for  .
It is helpful to define the
.
It is helpful to define the
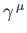 , for
, for 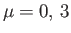 , where
, where
for 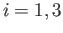 .
Equations (11.24)-(11.26) can then be shown to reduce to
.
Equations (11.24)-(11.26) can then be shown to reduce to
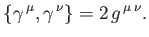 |
(11.29) |
(See Exercise 2.)
One way of satisfying the previous anti-commutation relations is to represent the operators
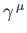 as matrices.
It follows that the operators
as matrices.
It follows that the operators 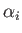 and
and 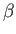 are also matrices.
[Incidentally, it is clear from Equation (11.21) that the
are also matrices.
[Incidentally, it is clear from Equation (11.21) that the 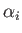 and
and 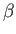 matrices must be Hermitian, otherwise
our effective Hamiltonian would not be an Hermitian operator.]
In fact, it is possible to prove that the
matrices must be Hermitian, otherwise
our effective Hamiltonian would not be an Hermitian operator.]
In fact, it is possible to prove that the 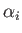 and
and 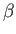 must be even-dimensional matrices. (See Exercise 3.)
Unfortunately, it is not possible to find a system of four appropriate
must be even-dimensional matrices. (See Exercise 3.)
Unfortunately, it is not possible to find a system of four appropriate 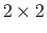 matrices. (The three Pauli
matrices have the correct properties, but there is no fourth matrix.)
It turns
out that the smallest dimension in which the
matrices. (The three Pauli
matrices have the correct properties, but there is no fourth matrix.)
It turns
out that the smallest dimension in which the
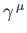 can be realized is four [9]. In fact, it is easily verified that the
can be realized is four [9]. In fact, it is easily verified that the 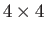 matrices
matrices
for 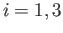 , satisfy the appropriate anti-commutation relations. (See Exercise 4) Here, 0
and
, satisfy the appropriate anti-commutation relations. (See Exercise 4) Here, 0
and 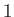 denote
denote 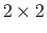 null and identity matrices, respectively, whereas the
null and identity matrices, respectively, whereas the 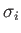 represent the
represent the 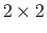 Pauli matrices
introduced in Section 5.7.
It follows from Equations (11.27) and (11.28) that
Pauli matrices
introduced in Section 5.7.
It follows from Equations (11.27) and (11.28) that
Note that
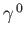 ,
, 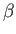 , and the
, and the 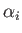 , are all Hermitian matrices, whereas the
, are all Hermitian matrices, whereas the
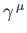 , for
, for 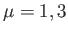 , are anti-Hermitian.
However, the matrices
, are anti-Hermitian.
However, the matrices
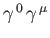 , for
, for 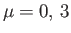 , are Hermitian. Moreover, it is easily demonstrated that
, are Hermitian. Moreover, it is easily demonstrated that
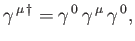 |
(11.34) |
for 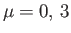 .
.
Equation (11.19) can be written in the form
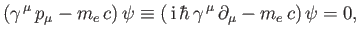 |
(11.35) |
where
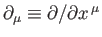 .
Alternatively, we can write
.
Alternatively, we can write
where
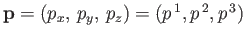 , and
, and
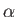 is the vector of the
is the vector of the 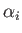 matrices. The previous expression is known as the Dirac equation [30].
Incidentally, it is clear that, corresponding to the four rows and columns of the
matrices. The previous expression is known as the Dirac equation [30].
Incidentally, it is clear that, corresponding to the four rows and columns of the
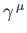 matrices, the wavefunction
matrices, the wavefunction 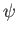 must take the form of a
must take the form of a 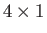 column matrix, each element of which is, in general, a function of the
column matrix, each element of which is, in general, a function of the 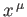 .
We saw in Section 5.7 that the spin of the electron requires the wavefunction to have two components. The reason
our present theory requires the wavefunction to have four components is because the wave equation (11.18) has twice
as many solutions as it ought to have, half of them corresponding to negative energy states.
.
We saw in Section 5.7 that the spin of the electron requires the wavefunction to have two components. The reason
our present theory requires the wavefunction to have four components is because the wave equation (11.18) has twice
as many solutions as it ought to have, half of them corresponding to negative energy states.
We can incorporate an electromagnetic field into the previous formalism by means of the standard prescription
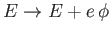 , and
, and
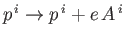 , where
, where 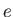 is the magnitude of the electron charge,
is the magnitude of the electron charge, 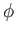 the scalar potential, and
the scalar potential, and 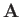 the
vector potential [67]. This prescription can be expressed in the Lorentz-invariant form
the
vector potential [67]. This prescription can be expressed in the Lorentz-invariant form
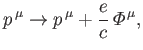 |
(11.37) |
where
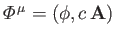 is the potential 4-vector [93]. Thus,
Equation (11.35) becomes
is the potential 4-vector [93]. Thus,
Equation (11.35) becomes
![$\displaystyle \left[\gamma^{\,\mu}\left(p_{\mu}+\frac{e}{c}\,{\mit\Phi}_{\mu}\r...
...hbar\,\partial_{\mu}+\frac{e}{c}\,{\mit\Phi}_{\mu}\right)-m_e\,c\right]\psi=0 ,$](img3881.png) |
(11.38) |
whereas
Equation (11.36) generalizes to
![$\displaystyle {\rm i}\,\hbar\,\frac{\partial\psi}{\partial t} =\left[-e\,\phi +...
...boldmath$\alpha$}\cdot({\bf p}+e\,{\bf A})+ \beta\,m_e\,c^{\,2}\right]\psi = 0.$](img3882.png) |
(11.39) |
If we write the wavefunction in the spinor form
![$\displaystyle \psi= \left(\begin{array}{c}\psi_0\\ [0.5ex]\psi_1\\ [0.5ex]\psi_2\\ [0.5ex]\psi_3\end{array}\right)$](img3883.png) |
(11.40) |
then the Hermitian conjugate of Equation (11.39) becomes
![$\displaystyle -{\rm i}\,\hbar\,\frac{\partial\psi^\dag }{\partial t} =\psi^\dag...
...x{\boldmath$\alpha$}\cdot({\bf p} +e\,{\bf A})+ \beta\,m_e\,c^{\,2}\right] = 0,$](img3884.png) |
(11.41) |
where
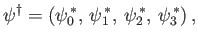 |
(11.42) |
Here, use has been made of the fact that the
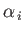 and the
and the 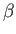 are Hermitian matrices that commute with the
are Hermitian matrices that commute with the 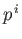 and the
and the 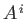 .
.
It follows from
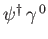 times Equation (11.38) that
times Equation (11.38) that
![$\displaystyle \psi^\dag\left[\gamma^{\,0}\,\gamma^{\,\mu}\left({\rm i}\,\hbar\,...
...l_{\mu}-\frac{e}{c}\,{\mit\Phi}_{\mu}\right)-\gamma^{\,0}\,m_e\,c\right]\psi=0.$](img3889.png) |
(11.43) |
The Hermitian conjugate of this expression is
![$\displaystyle \psi^\dag\left[\left(-{\rm i}\,\hbar\,\partial_{\mu}- \frac{e}{c}...
...}_{\mu}\right)\gamma^{\,0}\,\gamma^{\,\mu}-m_e\,c\,\gamma^{\,0}\,\right]\psi=0,$](img3890.png) |
(11.44) |
where
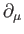 now acts backward on
now acts backward on 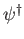 , and use has been made of the fact that the matrices
, and use has been made of the fact that the matrices
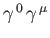 and
and
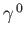 are Hermitian. Taking the difference between the previous two equations, we obtain
are Hermitian. Taking the difference between the previous two equations, we obtain
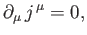 |
(11.45) |
where
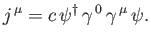 |
(11.46) |
Writing
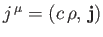 , where
, where
Equation (11.45) becomes
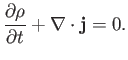 |
(11.49) |
The previous expression has the same form as the non-relativistic probability conservation equation, (3.65). This
suggests that we can interpret the positive-definite real scalar field
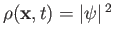 as the relativistic probability density, and the vector field
as the relativistic probability density, and the vector field
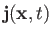 as the relativistic probability current. Integration of the preceding expression over all space, assuming that
as the relativistic probability current. Integration of the preceding expression over all space, assuming that
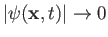 as
as
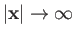 , yields
, yields
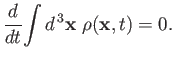 |
(11.50) |
This ensures that if the wavefunction is properly normalized at time  , such that
, such that
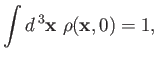 |
(11.51) |
then the wavefunction remains properly normalized at all subsequent times, as it evolves in accordance with the Dirac equation.
In fact, if this were not the case then it would be impossible to interpret 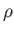 as a probability density. Now, relativistic
invariance demands that if the wavefunction is properly normalized in one particular inertial frame then it should
be properly normalized in all inertial frames [93]. This is the case provided that Equation (11.45) is Lorentz invariant (i.e., it has the property
that if it holds
in one inertial frame then it holds in all inertial frames),
which is true as long as the
as a probability density. Now, relativistic
invariance demands that if the wavefunction is properly normalized in one particular inertial frame then it should
be properly normalized in all inertial frames [93]. This is the case provided that Equation (11.45) is Lorentz invariant (i.e., it has the property
that if it holds
in one inertial frame then it holds in all inertial frames),
which is true as long as the 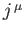 transform as the contravariant components of a 4-vector under Lorentz transformation. (See the following section, and Exercise 6.)
transform as the contravariant components of a 4-vector under Lorentz transformation. (See the following section, and Exercise 6.)



Next: Lorentz Invariance of Dirac
Up: Relativistic Electron Theory
Previous: Preliminary Analysis
Richard Fitzpatrick
2016-01-22
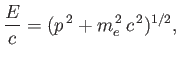
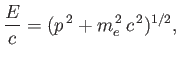
![]() , and is, thus, not of the form required by the laws of quantum theory. (Recall that we demonstrated, from
general principles, in Chapter 3, that the
time evolution equation for the wavefunction should be linear in the operator
, and is, thus, not of the form required by the laws of quantum theory. (Recall that we demonstrated, from
general principles, in Chapter 3, that the
time evolution equation for the wavefunction should be linear in the operator
![]() , and, hence, in
, and, hence, in ![]() .) We, therefore, seek a wave equation that is
equivalent to Equation (11.18), but is
linear in
.) We, therefore, seek a wave equation that is
equivalent to Equation (11.18), but is
linear in ![]() . In order to ensure that this equation transforms in a simple way under a Lorentz transformation, we
shall require it to be rational and linear in
. In order to ensure that this equation transforms in a simple way under a Lorentz transformation, we
shall require it to be rational and linear in ![]() ,
, ![]() ,
, ![]() , as well as
, as well as ![]() . We are, thus,
lead to a wave equation of the form
. We are, thus,
lead to a wave equation of the form
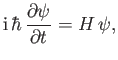
![$\displaystyle \left[p^{\,0}\,p^{\,0}-\frac{1}{2}\sum_{i,j=1,3}\{\alpha_i,\alpha...
...a_{\,i},\beta\}\,p^{\,i}\,m_e\,c-\beta^{\,2}\,m_e^{\,2}\,c^{\,2}\right]\psi= 0,$](img3847.png)
![]() , and
, and
![]() , where
, where ![]() is the magnitude of the electron charge,
is the magnitude of the electron charge, ![]() the scalar potential, and
the scalar potential, and ![]() the
vector potential [67]. This prescription can be expressed in the Lorentz-invariant form
the
vector potential [67]. This prescription can be expressed in the Lorentz-invariant form
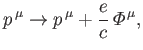
![$\displaystyle \psi= \left(\begin{array}{c}\psi_0\\ [0.5ex]\psi_1\\ [0.5ex]\psi_2\\ [0.5ex]\psi_3\end{array}\right)$](img3883.png)
![$\displaystyle -{\rm i}\,\hbar\,\frac{\partial\psi^\dag }{\partial t} =\psi^\dag...
...x{\boldmath$\alpha$}\cdot({\bf p} +e\,{\bf A})+ \beta\,m_e\,c^{\,2}\right] = 0,$](img3884.png)
![]() times Equation (11.38) that
times Equation (11.38) that
![$\displaystyle \psi^\dag\left[\gamma^{\,0}\,\gamma^{\,\mu}\left({\rm i}\,\hbar\,...
...l_{\mu}-\frac{e}{c}\,{\mit\Phi}_{\mu}\right)-\gamma^{\,0}\,m_e\,c\right]\psi=0.$](img3889.png)
![$\displaystyle \psi^\dag\left[\left(-{\rm i}\,\hbar\,\partial_{\mu}- \frac{e}{c}...
...}_{\mu}\right)\gamma^{\,0}\,\gamma^{\,\mu}-m_e\,c\,\gamma^{\,0}\,\right]\psi=0,$](img3890.png)