


Next: Resonant Scattering
Up: Scattering Theory
Previous: Hard-Sphere Scattering
In general, at low energies (i.e., when 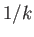 is much larger than the range
of the potential), partial waves with
is much larger than the range
of the potential), partial waves with 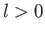 make a
negligible contribution to the scattering cross-section. It follows
that, with a finite-range potential, only S-wave (i.e., spherically symmetric)
scattering is important at such energies.
make a
negligible contribution to the scattering cross-section. It follows
that, with a finite-range potential, only S-wave (i.e., spherically symmetric)
scattering is important at such energies.
As a specific example, let us consider scattering by a finite
potential well, characterized by 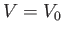 for
for 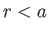 , and
, and
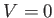 for
for 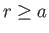 . Here,
. Here, 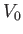 is a constant. The potential
is repulsive for
is a constant. The potential
is repulsive for 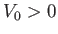 , and attractive for
, and attractive for 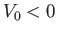 .
The external wavefunction is given by [see Equation (10.95)]
.
The external wavefunction is given by [see Equation (10.95)]
where use has been made of Equations (10.60) and (10.61).
The internal wavefunction follows from Equation (10.100). We obtain
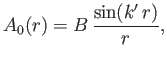 |
(10.119) |
where use has been made of the boundary condition (10.101).
Here, 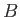 is a constant, and
is a constant, and
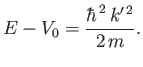 |
(10.120) |
Note that Equation (10.120) only applies when 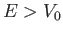 . For
. For 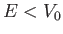 , we have
, we have
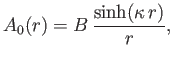 |
(10.121) |
where
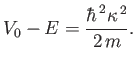 |
(10.122) |
Matching 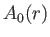 , and its radial derivative, at
, and its radial derivative, at  yields
yields
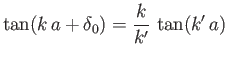 |
(10.123) |
for 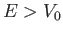 , and
, and
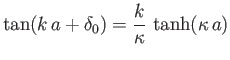 |
(10.124) |
for 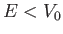 .
.
Consider an attractive potential, for which 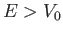 . Suppose that
. Suppose that
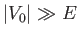 (i.e., the depth of the potential well is much larger than
the energy of the incident particles), so that
(i.e., the depth of the potential well is much larger than
the energy of the incident particles), so that 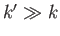 . As can be seen
from Equation (10.124), unless
. As can be seen
from Equation (10.124), unless
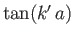 becomes extremely large, the right-hand side of the equation is much less than unity, so replacing the tangent of a
small quantity with the quantity itself, we obtain
becomes extremely large, the right-hand side of the equation is much less than unity, so replacing the tangent of a
small quantity with the quantity itself, we obtain
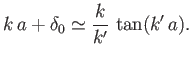 |
(10.125) |
This yields
![$\displaystyle \delta_0 \simeq k\,a \left[ \frac{\tan( k'\,a)}{k'\,a} -1\right].$](img3654.png) |
(10.126) |
According to Equation (10.115), the total scattering cross-section is given by
![$\displaystyle \sigma_{\rm total} \simeq \frac{4\pi}{k^{\,2}} \sin^2\delta_0 =4\pi \,a^{\,2}\left[\frac{\tan (k'\,a)}{k'\,a} -1\right]^{\,2}.$](img3655.png) |
(10.127) |
Now,
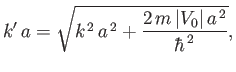 |
(10.128) |
so for sufficiently small values of 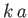 ,
,
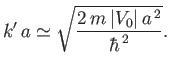 |
(10.129) |
It follows that the total (S-wave) scattering cross-section is independent
of the energy of the incident particles (provided that this energy is
sufficiently small).
Note that there are values of 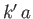 (e.g.,
(e.g.,
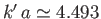 ) at which
the scattering cross-section (10.128) vanishes, despite the very strong
attraction of the potential. In reality, the cross-section is not
exactly zero, because of contributions from
) at which
the scattering cross-section (10.128) vanishes, despite the very strong
attraction of the potential. In reality, the cross-section is not
exactly zero, because of contributions from  partial waves. But,
at low incident energies, these contributions are small. It follows that
there are certain values of
partial waves. But,
at low incident energies, these contributions are small. It follows that
there are certain values of 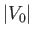 ,
, 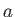 , and
, and 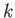 that give rise to almost perfect
transmission of the incident wave. This is called the Ramsauer-Townsend
effect, and has been observed experimentally [88,4].
that give rise to almost perfect
transmission of the incident wave. This is called the Ramsauer-Townsend
effect, and has been observed experimentally [88,4].



Next: Resonant Scattering
Up: Scattering Theory
Previous: Hard-Sphere Scattering
Richard Fitzpatrick
2016-01-22
![]() for
for ![]() , and
, and
![]() for
for ![]() . Here,
. Here, ![]() is a constant. The potential
is repulsive for
is a constant. The potential
is repulsive for ![]() , and attractive for
, and attractive for ![]() .
The external wavefunction is given by [see Equation (10.95)]
.
The external wavefunction is given by [see Equation (10.95)]
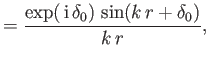
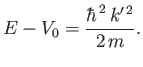
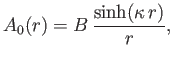
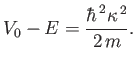
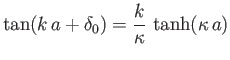
![]() . Suppose that
. Suppose that
![]() (i.e., the depth of the potential well is much larger than
the energy of the incident particles), so that
(i.e., the depth of the potential well is much larger than
the energy of the incident particles), so that ![]() . As can be seen
from Equation (10.124), unless
. As can be seen
from Equation (10.124), unless
![]() becomes extremely large, the right-hand side of the equation is much less than unity, so replacing the tangent of a
small quantity with the quantity itself, we obtain
becomes extremely large, the right-hand side of the equation is much less than unity, so replacing the tangent of a
small quantity with the quantity itself, we obtain
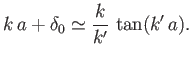
![$\displaystyle \delta_0 \simeq k\,a \left[ \frac{\tan( k'\,a)}{k'\,a} -1\right].$](img3654.png)
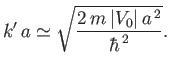
![]() (e.g.,
(e.g.,
![]() ) at which
the scattering cross-section (10.128) vanishes, despite the very strong
attraction of the potential. In reality, the cross-section is not
exactly zero, because of contributions from
) at which
the scattering cross-section (10.128) vanishes, despite the very strong
attraction of the potential. In reality, the cross-section is not
exactly zero, because of contributions from ![]() partial waves. But,
at low incident energies, these contributions are small. It follows that
there are certain values of
partial waves. But,
at low incident energies, these contributions are small. It follows that
there are certain values of ![]() ,
, ![]() , and
, and ![]() that give rise to almost perfect
transmission of the incident wave. This is called the Ramsauer-Townsend
effect, and has been observed experimentally [88,4].
that give rise to almost perfect
transmission of the incident wave. This is called the Ramsauer-Townsend
effect, and has been observed experimentally [88,4].