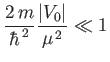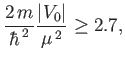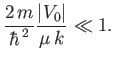

Next: Born Expansion
Up: Scattering Theory
Previous: Fundamental Equations
Born Approximation
Equation (10.28) is not particularly useful, as it stands, because the
quantity
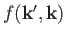 depends on the unknown ket
depends on the unknown ket
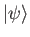 .
Recall that
.
Recall that
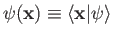 is the solution of the integral equation
is the solution of the integral equation
 |
(10.29) |
where
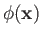 is the wavefunction of the incident state. [See Equation (10.13).]
According to the previous equation, the total wavefunction is a superposition
of the incident wavefunction and a great many spherical waves emitted from
the scattering region. The strength of the spherical wave emitted at
a given point in the scattering region is proportional to the local value of the scattering
potential,
is the wavefunction of the incident state. [See Equation (10.13).]
According to the previous equation, the total wavefunction is a superposition
of the incident wavefunction and a great many spherical waves emitted from
the scattering region. The strength of the spherical wave emitted at
a given point in the scattering region is proportional to the local value of the scattering
potential,
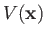 , as well as the local value of the wavefunction,
, as well as the local value of the wavefunction,
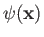 .
.
Suppose, however, that the scattering is not particularly intense. In this case, it is
reasonable to suppose that the total wavefunction,
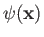 , does
not differ substantially from the incident wavefunction,
, does
not differ substantially from the incident wavefunction,
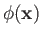 .
Thus, we can obtain an expression for
.
Thus, we can obtain an expression for
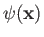 by making
the substitution
by making
the substitution
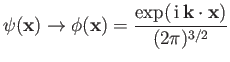 |
(10.30) |
on the right-hand side of Equation (10.29).
[See Equation (10.14).]
This simplification is known as the Born approximation [11].
The Born approximation yields
![$\displaystyle f({\bf k}', {\bf k}) \simeq - \frac{m}{2\pi\, \hbar^{\,2}} \int d...
...\,\exp\left[\, {\rm i}\, ({\bf k} - {\bf k}')\cdot {\bf x}'\right] V({\bf x}').$](img3467.png) |
(10.31) |
[See Equation (10.21).]
Thus,
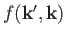 is proportional to the Fourier transform
of the scattering potential,
is proportional to the Fourier transform
of the scattering potential,
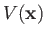 , with respect to the relative wavevector,
, with respect to the relative wavevector,
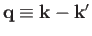 .
.
For a spherically symmetric scattering potential,
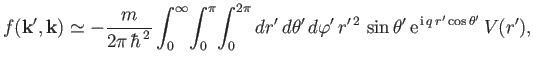 |
(10.32) |
giving
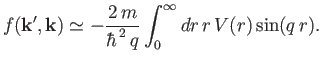 |
(10.33) |
Hence, it is clear that, for the special case of a
spherically symmetric potential,
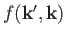 depends only on the magnitude of the relative wavevector,
depends only on the magnitude of the relative wavevector,
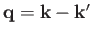 , and is independent of its direction.
Now, it is easily demonstrated that
, and is independent of its direction.
Now, it is easily demonstrated that
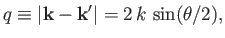 |
(10.34) |
where 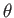 is the angle subtended between the vectors
is the angle subtended between the vectors
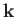 and
and 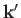 . In other words,
. In other words, 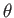 is the angle of
scattering. Recall that the
vectors
is the angle of
scattering. Recall that the
vectors 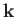 and
and 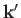 have the same length, as a consequence of energy conservation.
It follows that, according to the Born approximation,
have the same length, as a consequence of energy conservation.
It follows that, according to the Born approximation,
 for a spherically
symmetric scattering potential,
for a spherically
symmetric scattering potential,  . Moreover,
. Moreover, 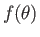 is real. Finally, the differential
scattering cross-section,
is real. Finally, the differential
scattering cross-section,
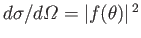 , is invariant under the transformation
, is invariant under the transformation
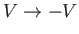 . In other words, the pattern of scattering is identical for attractive and repulsive
scattering potentials of the same strength.
. In other words, the pattern of scattering is identical for attractive and repulsive
scattering potentials of the same strength.
Consider scattering by a Yukawa potential [118],
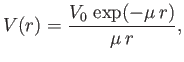 |
(10.35) |
where 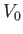 is a constant, and
is a constant, and  measures the ``range'' of the
potential. It follows from Equation (10.33) that
measures the ``range'' of the
potential. It follows from Equation (10.33) that
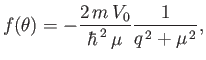 |
(10.36) |
because
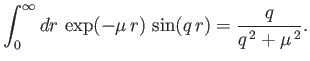 |
(10.37) |
(See Exercise 6.)
Thus, the Born approximation yields a differential cross-section
for scattering by a Yukawa potential of the form
![$\displaystyle \frac{d\sigma}{d {\mit\Omega}} \simeq \left(\frac{2\,m \,V_0}{ \h...
...right)^2 \frac{1}{\left[4\,k^{\,2}\,\sin^2(\theta/2) + \mu^{\,2}\right]^{\,2}}.$](img3482.png) |
(10.38) |
[See Equations (10.28) and (10.34).]
The Yukawa potential reduces to the familiar Coulomb potential in the limit
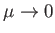 , provided that
, provided that
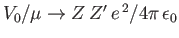 . Here,
. Here,  and
and 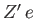 are the electric charges of the two interacting particles. In the Coulomb limit, the previous Born differential cross-section transforms into
are the electric charges of the two interacting particles. In the Coulomb limit, the previous Born differential cross-section transforms into
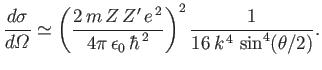 |
(10.39) |
Recalling that 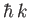 is equivalent to
is equivalent to 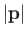 , where
, where 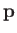 is the momentum of the incident particles, the preceding
equation can be rewritten
is the momentum of the incident particles, the preceding
equation can be rewritten
 |
(10.40) |
where
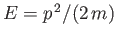 is the kinetic energy of the incident particles.
Equation (10.40) is identical to the well-known Rutherford scattering cross-section formula of classical physics [67].
is the kinetic energy of the incident particles.
Equation (10.40) is identical to the well-known Rutherford scattering cross-section formula of classical physics [67].
The Born approximation is valid provided
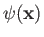 is
not significantly different from
is
not significantly different from
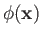 in the scattering region.
It follows, from Equation (10.29), that the condition that must be satisfied in order that
in the scattering region.
It follows, from Equation (10.29), that the condition that must be satisfied in order that
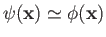 in the vicinity of
in the vicinity of
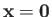 is
is
 |
(10.41) |
Consider the special case of the Yukawa potential, (10.35). At low energies
(i.e., 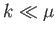 ), we can replace
), we can replace
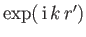 by unity,
giving
by unity,
giving
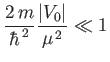 |
(10.42) |
as the condition for the validity of the Born approximation.
Now, the criterion for the Yukawa potential to develop a bound state
turns out to be
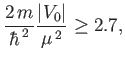 |
(10.43) |
provided 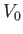 is negative [95]. Thus, if the potential is strong enough to
form a bound state then the Born approximation is likely to break
down. In the high-
is negative [95]. Thus, if the potential is strong enough to
form a bound state then the Born approximation is likely to break
down. In the high-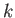 limit (i.e.,
limit (i.e., 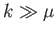 ), Equation (10.41) yields
), Equation (10.41) yields
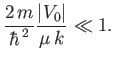 |
(10.44) |
This inequality becomes progressively easier to satisfy as 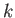 increases,
implying that the Born approximation becomes more accurate at high
incident particle energies
increases,
implying that the Born approximation becomes more accurate at high
incident particle energies


Next: Born Expansion
Up: Scattering Theory
Previous: Fundamental Equations
Richard Fitzpatrick
2016-01-22

![]() , does
not differ substantially from the incident wavefunction,
, does
not differ substantially from the incident wavefunction,
![]() .
Thus, we can obtain an expression for
.
Thus, we can obtain an expression for
![]() by making
the substitution
by making
the substitution
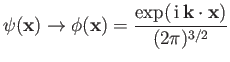
![$\displaystyle f({\bf k}', {\bf k}) \simeq - \frac{m}{2\pi\, \hbar^{\,2}} \int d...
...\,\exp\left[\, {\rm i}\, ({\bf k} - {\bf k}')\cdot {\bf x}'\right] V({\bf x}').$](img3467.png)
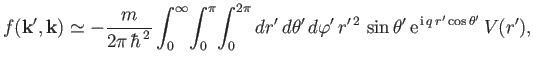
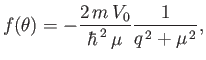
![]() , provided that
, provided that
![]() . Here,
. Here, ![]() and
and ![]() are the electric charges of the two interacting particles. In the Coulomb limit, the previous Born differential cross-section transforms into
are the electric charges of the two interacting particles. In the Coulomb limit, the previous Born differential cross-section transforms into
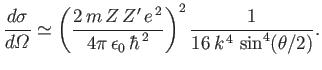
![]() is
not significantly different from
is
not significantly different from
![]() in the scattering region.
It follows, from Equation (10.29), that the condition that must be satisfied in order that
in the scattering region.
It follows, from Equation (10.29), that the condition that must be satisfied in order that
![]() in the vicinity of
in the vicinity of
![]() is
is