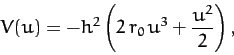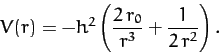Next: Motion in a Nearly
Up: Planetary Motion
Previous: Kepler Problem
Consider the motion of an object in a general (attractive) central force-field characterized by the potential energy per unit mass function  . Since the force-field
is central, it still remains true that
. Since the force-field
is central, it still remains true that
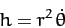 |
(299) |
is a constant of the motion. As is easily demonstrated, Equation (253)
generalizes to
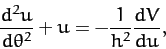 |
(300) |
where 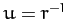 .
.
Suppose, for instance, that we wish to find the potential  which causes
an object to execute the spiral orbit
which causes
an object to execute the spiral orbit
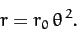 |
(301) |
Substitution of
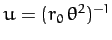 into Equation (300) yields
into Equation (300) yields
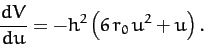 |
(302) |
Integrating, we obtain
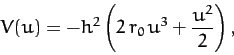 |
(303) |
or
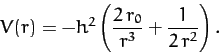 |
(304) |
In other words, the spiral pattern (301) is obtained from a mixture
of an inverse-square and inverse-cube potential.



Next: Motion in a Nearly
Up: Planetary Motion
Previous: Kepler Problem
Richard Fitzpatrick
2011-03-31
![]() which causes
an object to execute the spiral orbit
which causes
an object to execute the spiral orbit