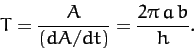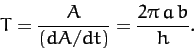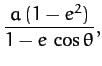Next: Orbital Energies
Up: Planetary Motion
Previous: Kepler's First Law
We have seen that the radius vector connecting our planet to the
origin sweeps out area at the constant rate 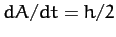 [see Equation (249)].
We have also seen that the planetary orbit is an ellipse. Suppose that
the major and minor radii of the ellipse are
[see Equation (249)].
We have also seen that the planetary orbit is an ellipse. Suppose that
the major and minor radii of the ellipse are 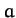 and
and 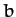 , respectively. It follows that the area of the ellipse is
, respectively. It follows that the area of the ellipse is 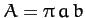 . Now, we expect the
radius vector to sweep out the whole area of the ellipse in a single
orbital period,
. Now, we expect the
radius vector to sweep out the whole area of the ellipse in a single
orbital period, 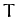 . Hence,
. Hence,
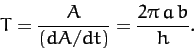 |
(257) |
It follows from Equations (236), (237), and (256)
that
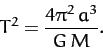 |
(258) |
In other words, the square of the orbital period of our planet is proportional to the cube
of its orbital major radius--this is Kepler's third law.
Note that for an elliptical orbit the closest distance to the Sun--the so-called
perihelion distance--is [see Equations (236) and (255)]
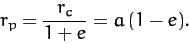 |
(259) |
Likewise, the furthest distance from the Sun--the so-called aphelion distance--is
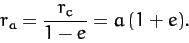 |
(260) |
It follows that the major radius, 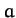 , is simply the mean of the perihelion
and aphelion distances,
, is simply the mean of the perihelion
and aphelion distances,
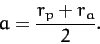 |
(261) |
The parameter
 |
(262) |
is called the eccentricity, and measures the deviation of the orbit
from circularity. Thus, 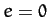 corresponds to a circular orbit, whereas
corresponds to a circular orbit, whereas
 corresponds to an infinitely elongated elliptical orbit.
corresponds to an infinitely elongated elliptical orbit.
As is easily demonstrated from the above analysis, Kepler laws of planetary motion can be written in the convenient form
where 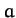 is the mean orbital radius (i.e., the major radius),
is the mean orbital radius (i.e., the major radius),  the orbital eccentricity, and
the orbital eccentricity, and
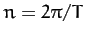 the mean orbital angular velocity.
the mean orbital angular velocity.



Next: Orbital Energies
Up: Planetary Motion
Previous: Kepler's First Law
Richard Fitzpatrick
2011-03-31