


Next: The Chaotic Pendulum
Up: Lunar Motion
Previous: Perturbed Lunar Motion
In order to better understand the perturbed lunar motion derived in the previous section, it is helpful to introduce the concept of
the mean moon. This is an imaginary body which orbits the Earth, in the ecliptic plane, at a
steady angular velocity that is equal to the Moon's mean orbital angular velocity, 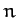 . Likewise, the
mean sun is a second imaginary body which orbits the Earth, in the ecliptic plane, at a
steady angular velocity that is equal to the Sun's mean orbital angular velocity,
. Likewise, the
mean sun is a second imaginary body which orbits the Earth, in the ecliptic plane, at a
steady angular velocity that is equal to the Sun's mean orbital angular velocity, 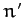 . Thus, the
ecliptic longitudes of the mean moon and the mean sun are
. Thus, the
ecliptic longitudes of the mean moon and the mean sun are
respectively. Here, for the sake of simplicity, and also for the sake of consistency with our
previous analysis, we have assumed that both objects are located at ecliptic longitude 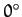 at time
at time  .
.
Now, from Equation (1213), to first-order in small parameters, the lunar perigee corresponds to
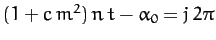 , where
, where
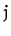 is an integer.
However, this condition can also be written
is an integer.
However, this condition can also be written
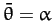 , where
, where
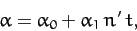 |
(1218) |
and, making use of Equation (1207), together with the definition 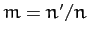 ,
,
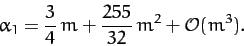 |
(1219) |
Thus, we can identify 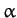 as the mean ecliptic longitude of the perigee. Moreover, according to Equation (1218),
the perigee precesses (i.e., its longitude increases in time) at the mean rate
of
as the mean ecliptic longitude of the perigee. Moreover, according to Equation (1218),
the perigee precesses (i.e., its longitude increases in time) at the mean rate
of 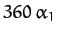 degrees per year. (Of course, a year corresponds to
degrees per year. (Of course, a year corresponds to
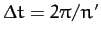 .) Furthermore, it is clear that this precession is entirely due to the perturbing influence of the Sun, since it only depends on the parameter
.) Furthermore, it is clear that this precession is entirely due to the perturbing influence of the Sun, since it only depends on the parameter 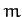 ,
which is a measure of this influence. Given that
,
which is a measure of this influence. Given that 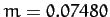 , we find that the perigee advances by
, we find that the perigee advances by
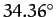 degrees per year. Hence, we predict that the perigee completes a full circuit about the Earth every
degrees per year. Hence, we predict that the perigee completes a full circuit about the Earth every
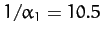 years.
In fact, the lunar perigee completes a full circuit every
years.
In fact, the lunar perigee completes a full circuit every 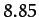 years. Our prediction is somewhat inaccurate because
our previous analysis neglected
years. Our prediction is somewhat inaccurate because
our previous analysis neglected 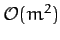 , and smaller, contributions to the parameter
, and smaller, contributions to the parameter 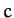 [see Equation (1207)],
and these turn out to be significant.
[see Equation (1207)],
and these turn out to be significant.
From Equation (1215), to first-order in small parameters, the Moon passes through its ascending node when
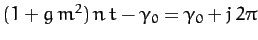 , where
, where
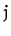 is an integer.
However, this condition can also be written
is an integer.
However, this condition can also be written
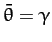 , where
, where
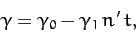 |
(1220) |
and, making use of Equation (1209),
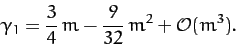 |
(1221) |
Thus, we can identify 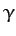 as the mean ecliptic longitude of the ascending node. Moreover, according to Equation (1220),
the ascending node regresses (i.e., its longitude decreases in time) at the mean rate
of
as the mean ecliptic longitude of the ascending node. Moreover, according to Equation (1220),
the ascending node regresses (i.e., its longitude decreases in time) at the mean rate
of 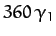 degrees per year. As before, it is clear that this regression is entirely due to the perturbing influence of the Sun. Moreover, we find that the ascending node retreats by
degrees per year. As before, it is clear that this regression is entirely due to the perturbing influence of the Sun. Moreover, we find that the ascending node retreats by
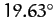 degrees per year. Hence, we predict that the ascending node completes a full circuit about the Earth every
degrees per year. Hence, we predict that the ascending node completes a full circuit about the Earth every
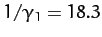 years.
In fact, the lunar ascending node completes a full circuit every
years.
In fact, the lunar ascending node completes a full circuit every 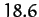 years, so our prediction is fairly accurate.
years, so our prediction is fairly accurate.
It is helpful to introduce the lunar mean anomaly,
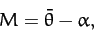 |
(1222) |
which is defined as the angular distance (in longitude) between the mean Moon and the perigee.
It is also helpful to introduce the lunar mean argument of latitude,
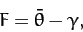 |
(1223) |
which is
defined as the angular distance (in longitude) between the mean Moon and the ascending node.
Finally, it is helpful to introduce the mean elongation of the Moon,
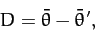 |
(1224) |
which is defined as the difference between the longitudes of the mean Moon and the mean Sun.
When expressed in terms of 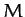 ,
, 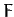 , and
, and 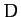 , our previous expression (1214) for the true ecliptic
longitude of the Moon becomes
, our previous expression (1214) for the true ecliptic
longitude of the Moon becomes
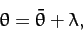 |
(1225) |
where
is the angular distance (in longitude) between the Moon and the mean Moon. The first three terms on the
right-hand side of the above expression are Keplerian (i.e., they are independent of the perturbing
action of the Sun). In fact, the first is due to the eccentricity of the lunar orbit (i.e., the fact that the
geometric center of the orbit is slightly shifted from the Earth), the second is due to
the ellipticity of the orbit (i.e., the fact that the orbit is slightly non-circular), and the third
is due to the slight inclination of the orbit to the ecliptic plane. However, the final two
terms are caused by the perturbing action of the Sun. In fact, the fourth term corresponds to
variation, whilst the fifth corresponds to evection. Note that variation attains its maximal
amplitude around the so-called octant points, at which the
Moon's disk is either one-quarter or three-quarters illuminated (i.e., when 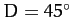 ,
, 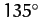 ,
,
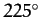 , or
, or 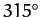 ). Conversely, the amplitude of variation is zero around the so-called quadrant points,
at which the Moon's disk is either fully illuminated, half illuminated, or not illuminated at all (i.e., when
). Conversely, the amplitude of variation is zero around the so-called quadrant points,
at which the Moon's disk is either fully illuminated, half illuminated, or not illuminated at all (i.e., when  ,
, 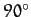 ,
,
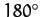 , or
, or 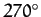 ). Evection can be thought of as causing a slight reduction in the eccentricity of the lunar
orbit around the times of the new moon and the full moon (i.e.,
). Evection can be thought of as causing a slight reduction in the eccentricity of the lunar
orbit around the times of the new moon and the full moon (i.e.,  and
and 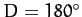 ), and
causing a corresponding slight increase in the eccentricity around the times of the first and last quarter moons
(i.e.,
), and
causing a corresponding slight increase in the eccentricity around the times of the first and last quarter moons
(i.e., 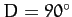 and
and 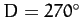 ). This follows because the evection term in Equation (1226) augments the eccentricity
term,
). This follows because the evection term in Equation (1226) augments the eccentricity
term, 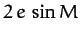 , when
, when 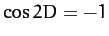 , and reduces the term when
, and reduces the term when 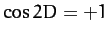 .
The variation and evection terms appearing in expression (1226) oscillate sinusoidally with periods of half a synodic month,
.
The variation and evection terms appearing in expression (1226) oscillate sinusoidally with periods of half a synodic month,![[*]](footnote.png) or
or 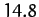 days, and
days, and 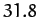 days, respectively. These periods are in good agreement with observations.
Finally, the amplitudes of the variation and evection terms (calculated using
days, respectively. These periods are in good agreement with observations.
Finally, the amplitudes of the variation and evection terms (calculated using 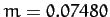 and
and 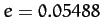 )
are
)
are 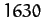 and
and 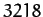 arc seconds, respectively. However, the observed amplitudes are
arc seconds, respectively. However, the observed amplitudes are
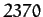 and
and 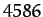 arc seconds, respectively. It turns out that our expressions for these amplitudes are somewhat inaccurate because, for the
sake of simplicity, we have only calculated the lowest order (in
arc seconds, respectively. It turns out that our expressions for these amplitudes are somewhat inaccurate because, for the
sake of simplicity, we have only calculated the lowest order (in 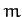 ) contributions to them. Recall that we also
neglected the slight eccentricity,
) contributions to them. Recall that we also
neglected the slight eccentricity, 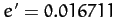 , of the Sun's apparent orbit about the
Earth in our calculation. In fact, the eccentricity of the solar orbit gives rise to a small addition term
, of the Sun's apparent orbit about the
Earth in our calculation. In fact, the eccentricity of the solar orbit gives rise to a small addition term
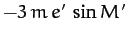 on the right-hand side of (1226),
where
on the right-hand side of (1226),
where 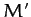 is the Sun's mean anomaly. This term, which is known as the annual equation, oscillates with a period
of a solar year, and has an amplitude of
is the Sun's mean anomaly. This term, which is known as the annual equation, oscillates with a period
of a solar year, and has an amplitude of 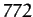 arc seconds.
arc seconds.
When expressed in terms of 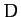 and
and 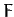 our previous expression (1215) for the ecliptic latitude of the Moon
becomes
our previous expression (1215) for the ecliptic latitude of the Moon
becomes
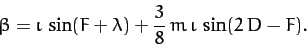 |
(1227) |
The first term on the right-hand side of this expression is Keplerian (i.e., it is independent of the perturbing
influence of the Sun). However, the final term, which is known as evection in latitude, is due to the
Sun's action. Evection in latitude can be thought of as causing a slight increase in the inclination of the lunar orbit
to the ecliptic at the times of the first and last quarter moons, and a slight decrease at the times of the new moon and
the full moon. The evection in latitude term oscillates sinusoidally with a period of 32.3 days, and has
an amplitude of 521 arc seconds. This period is in good agreement with observations. However, the observed
amplitude of the evection in latitude term is 624 arc seconds. As before, our expression for the amplitude is somewhat inaccurate because we have only calculated the lowest order (in 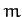 ) contribution.
) contribution.



Next: The Chaotic Pendulum
Up: Lunar Motion
Previous: Perturbed Lunar Motion
Richard Fitzpatrick
2011-03-31
![]() , where
, where
![]() is an integer.
However, this condition can also be written
is an integer.
However, this condition can also be written
![]() , where
, where
![]() , where
, where
![]() is an integer.
However, this condition can also be written
is an integer.
However, this condition can also be written
![]() , where
, where
![]() ,
, ![]() , and
, and ![]() , our previous expression (1214) for the true ecliptic
longitude of the Moon becomes
, our previous expression (1214) for the true ecliptic
longitude of the Moon becomes
![[*]](footnote.png) or
or ![]() and
and ![]() our previous expression (1215) for the ecliptic latitude of the Moon
becomes
our previous expression (1215) for the ecliptic latitude of the Moon
becomes